解:(1)
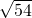
-

-
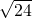
+

=3

-4

-2

+3

=

-

;
(2)(x-1)
2=4,
开方得:x-1=2或x-1=-2,
解得:x
1=3,x
2=-1;
(3)从三个代数式4x
2-y
2,2xy+y
2,4x
2+4xy+y
2中,任选两个4x
2-y
2,2xy+y
2,
构成的分式为
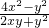
=
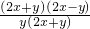
=
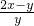
.
分析:(1)把第一项中的被开方数54变为9×6,第二项32变为16×2,第三项24变为4×6,第四项变为9×2,然后利用二次根式的乘法法则逆运算

=

•

化简,合并同类二次根式后即可得到结果;
(2)根据平方根的定义:一个数的平方等于a,这个数叫做a的平方根,根据4的平方根为±2,开方后得到关于x的方程,求出方程的解即可得到x的值,即为原方程的解,;
(3)从三个代数式中任取两个,构造为一个分式,例如取前两个,第一个作为分式的分子,第二个作为分式的分母,然后分别把分子分母分解因式,找出分子分母中的公因式,约分后得到最简结果.
点评:此题考查了二次根式的化简,直接开平方法解一元二次方程,以及分式的化简,二次根式的化简关键是合并同类二次根式,而合并的前提是必须将二次根式化为最简二次根式,利用直接开平方法解一元二次方程时,首先将方程左边化为一个完全平方式,右边为非负常数,然后根据平方根的定义将其转化为两个一元一次方程来求解;在对分式进行化简时,遇到分子分母是多项式时,应将多项式分解因式后再约分.

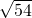 -
- -
-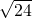 +
+
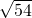 -
- -
-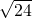 +
+
 -4
-4 -2
-2 +3
+3
 -
- ;
;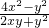 =
=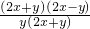 =
=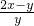 .
. =
= •
• 化简,合并同类二次根式后即可得到结果;
化简,合并同类二次根式后即可得到结果;

