
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H, tan∠AGB=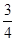 ,点G、A、C在同一条直线上.
,点G、A、C在同一条直线上.

(1)求证:EB⊥GD;
(2)若∠AG=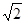 ,求BE的长.
,求BE的长.
(1)通过角度的转换求得各角的关系(2)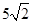
【解析】
试题分析:证明: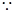 正方形AEFG、正方形ACBD
正方形AEFG、正方形ACBD
∴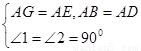
∴∠GAD=∠EAB
∴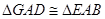 ..3分
..3分
∴∠4=∠3
∵∠4+∠GMA=900,
且∠GMA=∠EMH
∴∠3+∠EMH=900
∴BE⊥DG ……5分
(2)连接BD交AC于O,则AC⊥BD
∵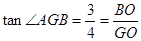
设BO=3x,则GO=4x
∴GA=4x-3x=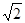
∴x=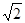
∴OD=OB=3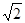 ,OG=4
,OG=4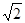
∴GD=5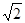 ,BD=6
,BD=6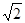 ……8分
……8分
由①得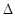 GAD
GAD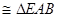
∴BE=GD=5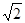
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
 (2012•龙湾区二模)如图,在Rt△AGB中,∠G=90°,∠A=30°,以GB为边在GB的下方作正方形GBEH,HE交AB于点F,以AB为边在AB的上方作正方形ABCD,连接CG,若GB=1,则CG2=
(2012•龙湾区二模)如图,在Rt△AGB中,∠G=90°,∠A=30°,以GB为边在GB的下方作正方形GBEH,HE交AB于点F,以AB为边在AB的上方作正方形ABCD,连接CG,若GB=1,则CG2=| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:[名校联盟]2013届重庆市重庆一中九年级下学期定时作业数学试卷(带解析) 题型:解答题
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H, tan∠AGB= ,点G、A、C在同一条直线上.
,点G、A、C在同一条直线上.
(1)求证:EB⊥GD;
(2)若∠AG=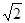 ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
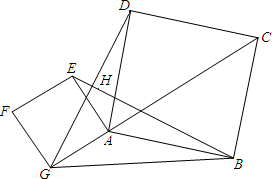 如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H,tan∠AGB=
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H,tan∠AGB= ,点G、A、C在同一条直线上.
,点G、A、C在同一条直线上. ,求BE的长.
,求BE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com