
已知,如图(甲),正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点,P不运动到M和C,以AB为直径做⊙O,过点P作⊙O的切线交AD于点F,切点为E.
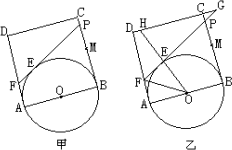
(1)求四边形CDFP的周长;
(2)试探索P在线段MC上运动时,求AF·BP的值;
(3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,使△EFO∽△EHG?如果存在,试求此时的BP的长;如果不存在,请说明理由.
|
(1)∵四边形ABCD是正方形∴∠A=∠B=90°, ∴AF、BP都是⊙O的切线, 又∵PF是⊙O的切线 ∴FE=FA,PE=PB ∴四边形CDFP的周长为: AD+DC+CB=2×3=6 (2)连结OE,PF是⊙O的切线 ∴OE⊥PF.在Rt△AOF和Rt△EOF中, ∵AO=EO,OF=OF ∴Rt△AOF≌Rt△EOF∴∠AOF=∠EOF, 同理∠BOP=∠EOP,∴∠EOF+∠EOP= 即OF⊥OP,∴AF·BP=EF·PE=OE2=1 (3)存在.∵∠EOF=∠AOF,∴∠EHG=∠AOE=2∠EOF, ∴当∠EFO=∠EHG=2∠EOF,即∠EOF=30°时,Rt△EFO∽Rt△EHG 此时,∠EOF=30°,∠BOP=∠EOP=90°-30°=60°∴BP=OB· |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
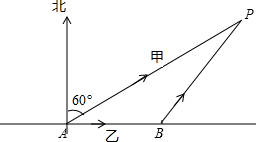 须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.
须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.查看答案和解析>>
科目:初中数学 来源: 题型:
 平面的夹角为30°,此时求:
平面的夹角为30°,此时求:查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 的夹角为30°,此时,求:
的夹角为30°,此时,求:查看答案和解析>>
科目:初中数学 来源: 题型:
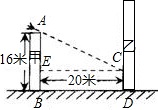
 如图,甲楼AB高18m,乙楼CD坐落在甲楼的正东面,已知当地冬至中午12时,物高与影长的比是1:
如图,甲楼AB高18m,乙楼CD坐落在甲楼的正东面,已知当地冬至中午12时,物高与影长的比是1:| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com