练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，阴影部分的面积为 (     )

    A.a2；      B.2a2；       C.a2；      D.a2.

     

    【答案】

    A

    【解析】

    试题分析：先根据题意得到扇形BEF的面积等于扇形CED的面积，即图形1的面积等于图形3的面积，通过割补的方法可知阴影部分的面积=图形1的面积+图形3的面积=正方形ABEF的面积．

    如图：

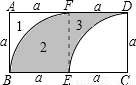
    四边形ABEF和四边形ECDF为正方形，且边长为a

    那么扇形BEF的面积等于扇形CED的面积

    所以图形1的面积等于图形3的面积

    则阴影部分的面积=图形1的面积+图形3的面积=正方形ABEF的面积=a2．

    考点：本题主要考查了通过割补法把不规则图形转化为规则图形求面积的方法

    点评：本题的关键是利用面积之间的等量代换得到阴影部分的面积=图形1的面积+图形3的面积=正方形ABEF的面积．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，阴影部分的面积相等的是（　　）
    精英家教网
    A、（2）（4）B、（1）（3）C、（2）（3）D、（1）（2）（3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，阴影部分的面积是（　　）
    A、
    11
    2
    xy
    B、
    9
    2
    xy
    C、4xy
    D、2xy

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    6、如图，阴影部分的面积为
    a2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网用代数式表示如图中阴影部分的面积，用计算器计算当a、b分别为0.38米与0.16米时，面积是多少？（π取3.14，结果保留两个有效数字）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，阴影部分的面积为
    1
    2
    ab-πr2
    1
    2
    ab-πr2
    ．

    查看答案和解析>>

    同步练习册答案