Question

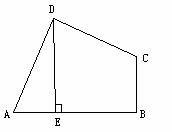
在四边形ABCD中,∠ADC=∠B=90⁰,DE⊥AB,垂足为E,AD=CD,且DE=BE=5,请用旋转图形的方法求四边形ABCD的面积.

Answer 1

解：把RtΔDEA以绕D按逆时针旋转90⁰，如图

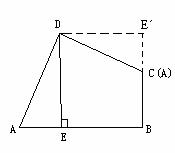
∵AD=CD ∴（A）与C重合

∴∠A=∠DCE′

∠E′=∠AED=90°

在四边形ABCD中

∵∠ADC=∠B=90°

∴∠A + ∠DCB = 180°

∴∠DCE′+ ∠DCB = 180°

即点B、C、E′在同一直线上

∵∠DEB = ∠E′=∠B=90°

∴四边形DEBE′是矩形

∴S_{矩形DEBE′}=DEBE

          = 55

          =25

∵S_{矩形DEBE′}=S_{四边形DEBC}+S_ΔDCE′

∵S_{四边形ABCD} = S_{四边形DEBC} + S_ΔADE

        = S_{四边形DEBC} + S_ΔDCE

∴S_{四边形ABCD} = S_矩形DEBE =25

答（略）