
函数常用的表示方法有三种.
已知A、B两地相距30千米,小王以40千米/时的速度骑摩托车从A地出发匀速前往B地参加活动.请选择两种方法来表示小王与B地的距离y(千米)与行驶时间x(小时)之间的函数关系.
科目:初中数学 来源: 题型:解答题
已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=- x+b,求n的值.
x+b,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
尔凡驾车从甲地到乙地,设他出发第xmin时的速度为ykm/h,图中的折线表示他在整个驾车过程中y与x之间的函数关系.
(1)当20≤x≤30时,汽车的平均速度为 km/h,该段时间行驶的路程为 km;
(2)当30≤x≤35时,求y与x之间的函数关系式,并求出尔凡出发第32min时的速度;
(3)如果汽车每行驶100km耗油8L,那么尔凡驾车从甲地到乙地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,直线 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P(2,
相交于点P(2, ).
).
(1)请判断 的形状并说明理由.
的形状并说明理由.
(2)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥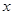 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数y=x -4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
-4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒。
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
| 画板的边长(dm) | 10 | 20 |
| 出售价(元/张) | 160 | 220 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知反比例函数 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, ),
),
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com