
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
分析 根据a2+|$\sqrt{50}$-c|=10a-25-$\sqrt{5-b}$得到(a-5)2+|$\sqrt{50}$-c|+$\sqrt{5-b}$=0,然后利用非负数的性质得到a=5,b=5,c=$\sqrt{50}$,从而利用勾股定理逆定理判定该三角形为等腰直角三角形.
解答 解:∵a2+|$\sqrt{50}$-c|=10a-25-$\sqrt{5-b}$,
∴a2-10a+25+|$\sqrt{50}$-c|+$\sqrt{5-b}$=0,
即(a-5)2+|$\sqrt{50}$-c|+$\sqrt{5-b}$=0,
∴a=5,b=5,c=$\sqrt{50}$,
∵a2+b2=25+25=50=($\sqrt{50}$)2=c2,
∴该三角形为等腰直角三角形,
故选C.
点评 本题考查了配方法的应用及绝对值等非负数的性质,解题的关键是能够将原式进行配方,难度不大.


科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:判断题
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
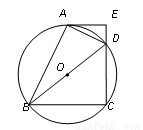
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 购票人数 | 1-30人 | 31-60人 | 60人以上 |
| 票价 | 无折扣 | 超出30人的部分,票价打八折 | 超出60人的部分,票价打五折 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | a2 | C. | -a | D. | $\frac{1}{a^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
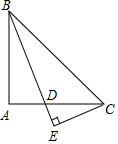 已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
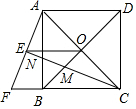 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
下列运算中,正确的是( )
A. 4x+3y=7xy B. 3x2+2=5x2
C. 6xy-4xy=2xy D. 5x2-x2=4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com