
已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.

(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°- ∠FCM.[来源:ZXXK][来源:学|科|网Z|X|X|K]
(1)连结MD
∵点E是DC的中点,ME⊥DC ∴MD=MC
又∵AD=CF,MF=MA ∴△AMD≌△FMC
∴∠MAD=∠MFC=120° ∵AD∥BC,∠ABC=90°
∴∠BAD=90° ∴∠MAB=30°
在Rt△AMB中,∠MAB=30°
∴BM=AM.,即AM=2BM
(2)∵△AMD≌△FMC ∴∠ADM=∠FCM
∵AD∥BC ∴∠ADM=∠CMD
∴∠CMD=∠FCM
∵MD=MC,ME⊥DC
∴∠DME==∠CME=∠CMD
∴∠CME=∠FCM
在在Rt△MBP中,∠MPB=90°-∠CME=90°- ∠FCM
【解析】(1)连接MD,由于点E是DC的中点,ME⊥DC,所以MD=MC,然后利用已知条件证明△AMD≌△FMC,根据全等三角形的性质可以推出∴∠MAD=∠MFC=120°,接着得到∠MAB=30°,再根据30°的角所对的直角边等于斜边的一半即可证明AM=2BM;
(2)利用(1)的结论得到∠ADM=∠FCM,又AD∥BC,所以∠ADM=∠CMD,由此得到∠CMD=∠FCM,再利用等腰三角形的性质即可得到∠CME=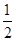 ∠FCM,再根据已知条件即可解决问题.
∠FCM,再根据已知条件即可解决问题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2011年河南省周口市初一下学期相交线与平行线专项训练 题型:解答题
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,建立平面直角坐标系.已知OA=4,OB=3,一动点P从O出发沿OA方向,以每秒1个
单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动.当Q到达B时,P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t>0).
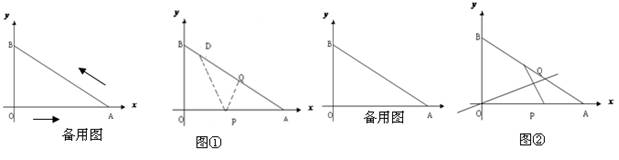
(1) 试求出△APQ的面积S与运动时间t之间的函数关系式;
(2) 在某一时刻将△APQ沿着PQ翻折,使得点A恰好落在AB边的点D处,如图①.
求出此时△APQ的面积.
(3) 在点P从O向A运动的过程中,在y轴上是否存在着点E使得四边形PQBE为等腰梯
形?若存在,求出点E的坐标;若不存在,请说明理由.
(4) 伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F. 当DF经过原点O时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源:2011年河南省周口市初一下学期平移专项训练 题型:解答题
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,建立平面直角坐标系.已知OA=4,OB=3,一动点P从O出发沿OA方向,以每秒1个
单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动.当Q到达B时,P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t>0).

(1) 试求出△APQ的面积S与运动时间t之间的函数关系式;
(2) 在某一时刻将△APQ沿着PQ翻折,使得点A恰好落在AB边的点D处,如图①.
求出此时△APQ的面积.
(3) 在点P从O向A运动的过程中,在y轴上是否存在着点E使得四边形PQBE为等腰梯
形?若存在,求出点E的坐标;若不存在,请说明理由.
(4) 伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F. 当DF经过原点O时,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com