
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )

A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
【答案】D
【解析】试题分析 :①、∵AB是⊙O的直径,
由直径所对圆周角是直角得∠ADB=90°,
即AD⊥BD,
故①成立;
②、∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
∴∠AOC≠∠AEC,
故②不成立;
③、∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,
故③成立;
④、∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,
故④成立;
⑤、由④有,AF=DF,
∵点O为AB中点,
∴OF是△ABD的中位线,
∴BD=2OF,
故⑤成立;
⑥∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故⑥不成立.
故选D.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】(本题10分)我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为C1,把锅盖纵断面的抛物线记为C2.
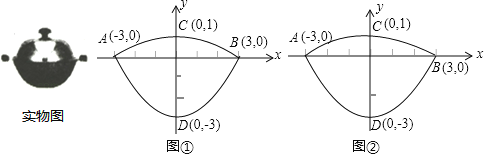
(1)求C1和C2的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式组![]() 无解,则a的取值范围是__.
无解,则a的取值范围是__.
【答案】a≥7
【解析】![]()
解①得
![]() ;
;
解②得
![]() ;
;
∵不等式组无解,
∴a≥7.
点睛:本题考查了一元一次不等式组的知识,解一元一次不等式组的应用,解此题的关键是能根据不等式组无解得出关于m的不等式组.
【题型】填空题
【结束】
21
【题目】解不等式组:![]() ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的10亩杂交水稻的产量进行了检测,在这个问题中10是( )
A.个体
B.总体
C.总体的样本
D.样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com