
 已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )
已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )| A. |  | B. |  | C. |  | D. | 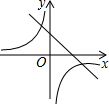 |
分析 根据二次函数图象可知“a>0,b<0,c<0”,由此即可判定出一次函数、反比例函数图象所在的象限,结合四个选项即可得出结论.
解答 解:∵抛物线开口向上,
∴a>0;
∵抛物线对称轴大于0,即-$\frac{b}{2a}$>0,
∴ab<0,
∴b<0;
∵抛物线与y轴的交点在负半轴,
∴c<0.
当a>0,b<0时,一次函数y=ax+b的图象过第一、三、四象限;
当c<0时,反比例函数图象在第二、四象限.
故选C.
点评 本题考查了二次函数的图象、一次函数的图象以及反比例函数的图象,解题的关键是找出“a>0,b<0,c<0”.本题属于基础题,难度不大,解决该题型题目时,根据二次函数图象得出系数a、b、c的符号是关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
 如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点,当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”.否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1,因此这两个函数在-3≤x≤-1上是“相邻函数”.
如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点,当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”.否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1,因此这两个函数在-3≤x≤-1上是“相邻函数”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30$\sqrt{6}$海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30$\sqrt{6}$海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.41×104 | B. | 41×104 | C. | 4.1×106 | D. | 4.1×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A是双曲线y=$\frac{8}{x}$(x>0)上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y=$\frac{2}{x}$(x>0)于点B、C,连接BC,设点A的横坐标为a.
如图,点A是双曲线y=$\frac{8}{x}$(x>0)上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y=$\frac{2}{x}$(x>0)于点B、C,连接BC,设点A的横坐标为a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com