解:
(1)令x=0,y=4,
令y=0,则-

x+4=0,
解得x=3,
所以,A(0,4),B(3,0),
由勾股定理得,AB=

=5,
BD=
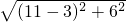
=10,
过点D作DH⊥y轴于H,DH=11,AH=2,
由勾股定理得,AD=

=
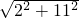
=
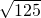
,
∵AB
2=25,BD
2=100,
∴AB
2+BD
2=AD
2,
∴△ABD是直角三角形;
(2)设OC长为x,由等腰三角形以及勾股定理得到x
2+4
2=(11-x)
2+6
2,
解得x=
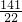
,
所以,C(
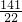
,0);
(3)设t秒时相遇,由题意得,t+t=5+10,
解得t=7.5,
点P在AB上时,0≤t≤5,PB=5-t,BQ=10-t,
PQ=
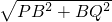
=
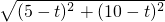
=
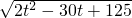
,
点P、Q都在BD上重合前,5<t≤7.5,PQ=5+10-t-t=15-2t,
重合后,7.5<t≤10,PQ=t+t-5-10=2t-15,
点Q在AB上时,10<t≤5,PB=t-5,BQ=t-10,
PQ=
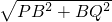
=
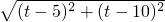
=
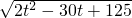
.
分析:(1)令x=0,y=0分别求解即可得到点A、B的坐标,然后利用勾股定理列式计算即可得到AB、BD,过点D作DH⊥y轴于H,然后求出DH、AH,再利用勾股定理列式计算求出AD,然后根据勾股定理逆定理证明即可;
(2)设OC=x,根据等腰三角形两腰相等利用勾股定理列出方程求解即可;
(3)求出点P、Q相遇时的t值,然后分点P在AB上,点P、Q都在BD上重合前和重合后两种情况,点Q在AB上四种情况讨论求解.
点评:本题是一次函数综合题型,主要利用了一次函数与坐标轴的交点的求解方法,勾股定理的应用,等腰三角形两腰相等的性质,难点在于(3)要分情况讨论.

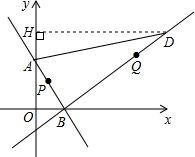
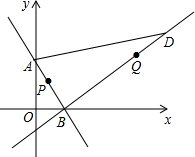 已知直线y=-
已知直线y=- x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).
x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6). (1)令x=0,y=4,
(1)令x=0,y=4, x+4=0,
x+4=0, =5,
=5,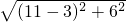 =10,
=10, =
=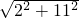 =
=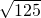 ,
,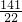 ,
,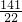 ,0);
,0);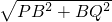 =
=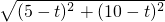 =
=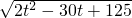 ,
,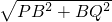 =
=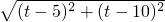 =
=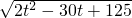 .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案