
 如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.
如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.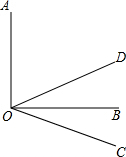 解:(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,
解:(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 日期(10月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人数变化(万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,将△ABC绕顶点C旋转,点A转到BC边上的点E处,点B转到点F处,延长FE交AB于点D,则S△BED=( )
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,将△ABC绕顶点C旋转,点A转到BC边上的点E处,点B转到点F处,延长FE交AB于点D,则S△BED=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.
某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.. |
| x |
| x1+x2+…+xn |
| n |
. |
| x |
| 4+5+6+7 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是( )
如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是( )| A、3cm | B、4cm |
| C、5cm | D、6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com