
 = .
= .
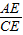 =tan∠ADM=
=tan∠ADM=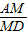 .设等腰直角三角形的直角边是1,因而AC=AB=1,易证DM∥AB,△CDM∽△CBA,因而AM=
.设等腰直角三角形的直角边是1,因而AC=AB=1,易证DM∥AB,△CDM∽△CBA,因而AM= ,DM=
,DM= ,因而
,因而 =
= ,则
,则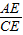 =
= .
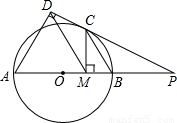
. 解:过点D作DM⊥AC,∵CE⊥AD,
解:过点D作DM⊥AC,∵CE⊥AD, =tan∠ADM=
=tan∠ADM= .
. ,DM=
,DM= ,
,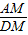 =
= ,
, =
= .
. .
.

科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(07)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(05)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(01)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《三角形》(05)(解析版) 题型:解答题
 BC,CF=12,求AF的长.
BC,CF=12,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com