D
分析:根据题意,分析分别就a、当x≥0、y≥0时;b、当x≥0、y≤0时;c、当x≤0、y≥0时;当x≤0、y≤0时四种情况,去掉决定值符号,分解因式联立方程,利用根据与系数的关系即是否符号题意,来判断方程组的解.
解答:
a、当x≥0、y≥0时,
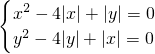
?
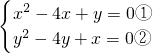
由①-②得 x
2-y
2-5(x+y)=0?(x+y)(x-y-5)=0,即x=-y或 x=y+5 ③
当x=-y时,解得x=0,y=0,
当x=y+5时,②③联立得 y
2-3y+5=0
∵△=9-20=-11<0,
∴无解.
b、当x≥0、y≤0时,
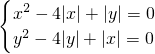
?
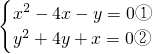
由①-②得 x
2-y
2-5(x+y)=0?(x+y)(x-y-5)=0,即x=-y或x=y+5 ③
当x=-y时,②③联立得 y
2+3y=0
解得
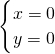
或
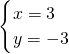
当x=y+5时,②③联立得 y
2-3y+5=0
∵△=9-20=-11<0,
∴无解.
c、当x≤0、y≥0时,
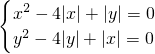
?
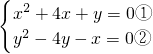
由①-②得 x
2-y
2+5(x+y)=0?(x+y)(x-y+5)=0,即x=-y或x=y-5 ③
当x=-y时,②③联立得 y
2-3y=0
解得
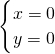
或
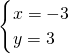
,
当x=y-5时,②③联立得 y
2-5y+5=0
∵△=25-20=45>0,
∴方程有两解.
d、当x≤0、y≤0时,
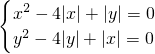
?
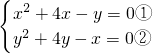
由①-②得 x
2-y
2+5(x-y)=0?(x-y)(x+y-5)=0,即x=y或x=-y+5 ③
当x=y时,②③联立得 y
2+3y=0
解得
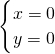
或
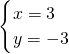
(不合题意,舍去)
当x=-y+5时,②③联立得 y
2+5y-5=0
∵△=25+20=45>0,
∴方程有两解.
综上所述,方程有5个解.
故选D.
点评:本题考查高次方程.解决本题一定要考虑全面,不必解出具体解,只要判断解的个数即可.

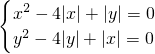 在实数范围内
在实数范围内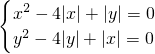 ?
?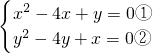
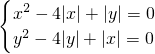 ?
?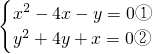
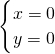 或
或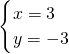
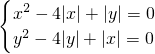 ?
?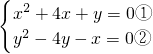
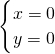 或
或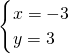 ,
,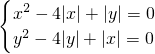 ?
?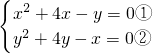
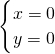 或
或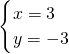 (不合题意,舍去)
(不合题意,舍去)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案