
 的图象上,则k的值为________.
的图象上,则k的值为________. ,
,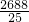 ,
,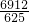
 ,即可求出k的值.由于AB=5,所以当Rt△ABC的三边长均为整数时,分AB为斜边和AB为直角边进行讨论:①如果AB=5为斜边,那么两条直角边分别为3,4.当AC=3时,易求C(4,3);当BC=3时,根据直角三角形的性质及三角函数的定义,可求出C(
,即可求出k的值.由于AB=5,所以当Rt△ABC的三边长均为整数时,分AB为斜边和AB为直角边进行讨论:①如果AB=5为斜边,那么两条直角边分别为3,4.当AC=3时,易求C(4,3);当BC=3时,根据直角三角形的性质及三角函数的定义,可求出C( ,
, );②如果AB=5为直角边,那么另外两条边分别为12,13.当AC=12时,根据相似三角形的判定与性质可求C(
);②如果AB=5为直角边,那么另外两条边分别为12,13.当AC=12时,根据相似三角形的判定与性质可求C( ,
, );当BC=12时,根据相似三角形的判定与性质可求C(
);当BC=12时,根据相似三角形的判定与性质可求C( ,
,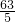 ).
). 解:∵A(4,0),B(0,3),
解:∵A(4,0),B(0,3), .
. ,
,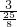 =
= ,C2D=BC2•sin∠C2BD=BC2•sin∠C1AP=3×
,C2D=BC2•sin∠C2BD=BC2•sin∠C1AP=3×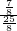 =
=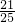 ,
,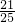 =
= ,
, ∴C2点坐标为(
∴C2点坐标为( ,
, ),
), ×
× =
=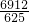 ;
; ,DA=
,DA= ,
, =
= ,
,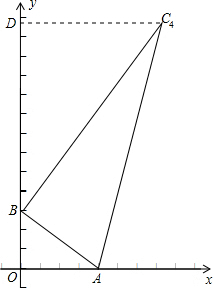 ∴C3点坐标(
∴C3点坐标( ,
, ),
), ×
× =
=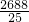 ;
; ,DB=
,DB= ,
, =
=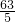 ,
, ,
,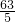 ),
), ×
×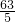 =
= .
. ,
,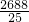 ,
,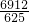 .
. ,
,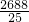 ,
,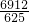 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
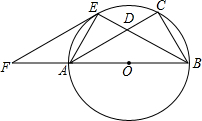 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:
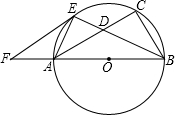 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:
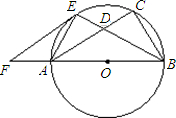 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
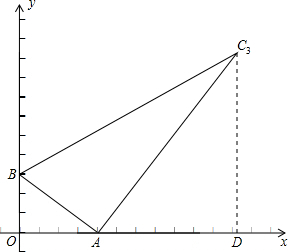
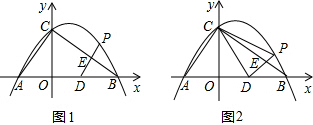 已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).
已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com