
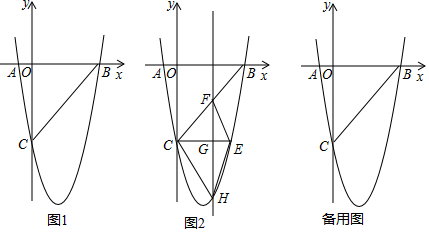
���� ��1�����ݴ���ϵ����ֱ��ȷ���������߽���ʽ��
��2��������������������������εı���ʽ���������D�����ꣻ
��3�������ֱ��BC�Ľ���ʽ����������ı���CHEF������ĺ�����ϵʽ������������ֵ��
��4�����öԳ����ҳ���P��Q��λ�ã��������P��Q�����꣮
��� �⣺��1���ߵ�A��-1��0����B��5��0����������y=ax2+bx-5�ϣ�
��$\left\{\begin{array}{l}{a-b-5=0}\\{25a+5b-5=0}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=1}\\{b=-4}\end{array}\right.$��
�������ߵı���ʽΪy=x2-4x-5��
��2����ͼ1��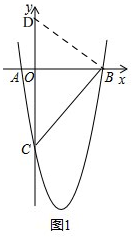 ��x=0����y=-5��
��x=0����y=-5��
��C��0��-5����
��OC=OB��
���OBC=��OCB=45�㣬
��AB=6��BC=5$\sqrt{2}$��
Ҫʹ��B��C��DΪ��������������ABC���ƣ�����$\frac{AB}{CD}=\frac{BC}{BC}$��$\frac{AB}{BC}=\frac{BC}{CD}$��
�ٵ�$\frac{AB}{CD}=\frac{BC}{BC}$ʱ��
CD=AB=6��
��D��0��1����
�ڵ�$\frac{AB}{BC}=\frac{BC}{CD}$ʱ��
��$\frac{6}{5\sqrt{2}}=\frac{5\sqrt{2}}{CD}$��
��CD=$\frac{25}{3}$��
��D��0��$\frac{10}{3}$����
����D��������0��1����0��$\frac{10}{3}$����
��3����H��t��t2-4t-5����
��CE��x�ᣬ
���E��������Ϊ-5��
��E���������ϣ�
��x2-4x-5=-5��
��x=0���ᣩ��x=4��
��E��4��-5����
��CE=4��
��B��5��0����C��0��-5����
��ֱ��BC�Ľ���ʽΪy=x-5��
��F��t��t-5����
��HF=t-5-��t2-4t-5��=-��t-$\frac{5}{2}$��2+$\frac{25}{4}$��
��CE��x�ᣬHF��y�ᣬ
��CE��HF��
��S�ı���CHEF=$\frac{1}{2}$CE•HF=-2��t-$\frac{5}{2}$��2+$\frac{25}{2}$��
��t=$\frac{5}{2}$ʱ���ı���CHEF��������Ϊ$\frac{25}{2}$��
��t=$\frac{5}{2}$ʱ��t2-4t-5=$\frac{25}{4}$-10-5=-$\frac{35}{4}$��
��H��$\frac{5}{2}$��-$\frac{35}{4}$����
��4����ͼ2��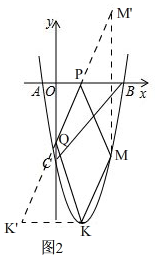 ��KΪ�����ߵĶ��㣬
��KΪ�����ߵĶ��㣬
��K��2��-9����
��K����y��ĶԳƵ�K'��-2��-9����
��M��4��m�����������ϣ�
��M��4��-5����
���M����x��ĶԳƵ�M'��4��5����
��ֱ��K'M'�Ľ���ʽΪy=$\frac{7}{3}$x-$\frac{13}{3}$��
��P��$\frac{13}{7}$��0����Q��0��-$\frac{13}{3}$����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������������ε��ж������ʣ��ı��ε�����ļ��㷽�����Գ��ԣ���ֵ��ȷ�����⣨2���Ĺؼ��Ƿ������ۣ��⣨3���Ĺؼ��DZ�ʾ��HF���⣨4���Ĺؼ������öԳ����ҳ���P��Q��λ�ã���һ���е��Ѷȵ���Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
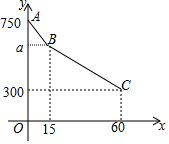 ��ĩ��С����ҽԺ���չ�������Һ��С���ʣ���������������Һ�ٶȣ�����ʱ���ܽ�����Һ�������ϴ𣺡�75���ӣ���15���Ӻ�С����������Һ���ٶȣ�60���Ӻ�С�����ֻ�ʣ��300����ҩҺ��ʣ�´���ҩҺy������������Һʱ��x�����ӣ��ĺ�����ϵ��ͼ��ʾ��
��ĩ��С����ҽԺ���չ�������Һ��С���ʣ���������������Һ�ٶȣ�����ʱ���ܽ�����Һ�������ϴ𣺡�75���ӣ���15���Ӻ�С����������Һ���ٶȣ�60���Ӻ�С�����ֻ�ʣ��300����ҩҺ��ʣ�´���ҩҺy������������Һʱ��x�����ӣ��ĺ�����ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
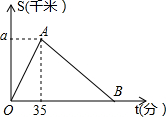 ij�˶�Ա����㶫ʤһ�г�������ֲ�����ر���·���ܻض�ʤһ�У�����˶�Ա�뿪����·��S��ƽ�ף����ܲ�ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ�����д���㵽ֲ����ƽ���ٶ���0.4ǧ��/�֣���ʱ35���ӣ�����ͼ���ṩ����Ϣ������������⣺
ij�˶�Ա����㶫ʤһ�г�������ֲ�����ر���·���ܻض�ʤһ�У�����˶�Ա�뿪����·��S��ƽ�ף����ܲ�ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ�����д���㵽ֲ����ƽ���ٶ���0.4ǧ��/�֣���ʱ35���ӣ�����ͼ���ṩ����Ϣ������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
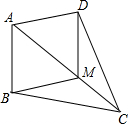 �ڡ�ABC�У�M��AC���ϵ�һ�㣬����BM������ABC��AC���ۣ�ʹ��B���ڵ�D������DM��ABʱ����֤���ı���ABMD�����Σ�
�ڡ�ABC�У�M��AC���ϵ�һ�㣬����BM������ABC��AC���ۣ�ʹ��B���ڵ�D������DM��ABʱ����֤���ı���ABMD�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ز����� | ���� | �ն��� | �ʻ��� |
| ÿ���������������֣� | 8 | 6 | 5 |
| ÿ���ز�������Ԫ�� | 1.2 | 1.6 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
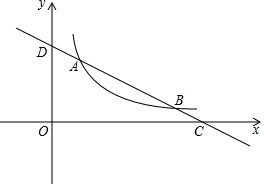 ��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��x��0������A��2��4����B��a��1������x�ᣬy��ֱ��ڵ�C��D��
��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��x��0������A��2��4����B��a��1������x�ᣬy��ֱ��ڵ�C��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
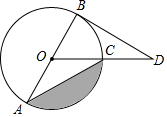 ��ͼ��BD�ǡ�O�����ߣ�BΪ�е㣬����DO���O���ڵ�C��ABΪ��O��ֱ��������CA������D=30�㣬��O�İ뾶Ϊ4����ͼ����Ӱ���ֵ����Ϊ$\frac{16}{3}��-4\sqrt{3}$��
��ͼ��BD�ǡ�O�����ߣ�BΪ�е㣬����DO���O���ڵ�C��ABΪ��O��ֱ��������CA������D=30�㣬��O�İ뾶Ϊ4����ͼ����Ӱ���ֵ����Ϊ$\frac{16}{3}��-4\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
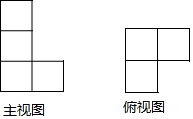 һ�������������ͼ����ͼ��ͼ��ʾ������������������a��С��������ɣ�������b��С��������ɣ���a+b���ڣ�������
һ�������������ͼ����ͼ��ͼ��ʾ������������������a��С��������ɣ�������b��С��������ɣ���a+b���ڣ�������| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com