
 +tan45°;
+tan45°;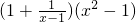 ,其中x=
,其中x= .
.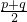 ,G=
,G=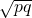 .而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足
.而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足 -
- =
= -
- ,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数.
,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数. +1+
+1+ +1,
+1, +1+
+1+ -1+1,
-1+1, +
+ ;
; •(x+1)(x-1),
•(x+1)(x-1), 时,原式=(
时,原式=( )2+
)2+ =
= ;
;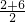 =4;G=
=4;G= =2
=2 ;
; ;
; -
-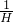 =
=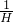 -
- ,
,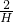 =
= +
+ ,
,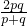 ,
,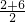 =4;G=
=4;G= =2
=2 ;
; -
-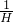 =
=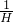 -
- ,整理得到H=
,整理得到H=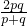 ,然后任意取p,q的值,通过计算得到H,这样就可得到一组调和数.
,然后任意取p,q的值,通过计算得到H,这样就可得到一组调和数.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com