
 ijУ�о���ѧϰС���ԡ�ѧ����ѧУ��ͨ�������͡�Ϊ�����ȫУѧ����������������飬�������Ŀ�У�����������С����Ħ�г������г���������ÿλͬѧ��ѡһ������ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
ijУ�о���ѧϰС���ԡ�ѧ����ѧУ��ͨ�������͡�Ϊ�����ȫУѧ����������������飬�������Ŀ�У�����������С����Ħ�г������г���������ÿλͬѧ��ѡһ������ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��| ��ͨ��ʽ | Ƶ���������� | Ƶ�� |
| �������� | m | 0.25 |
| �� | 24 | 0.20 |
| Ħ�г� | 36 | n |
| ���г� | 18 | 0.15 |
| ���� | 12 | 0.10 |
���� ��1������Ƶ��=$\frac{Ƶ��}{��������}$���м��㣻
��2������Ƶ��=$\frac{Ƶ��}{��������}$���м��㣻
��3������������ͳ��ͼ�У�ÿ����ռ�ܲ��ֵİٷֱȵ��ڸò�������Ӧ������Բ�ĽǵĶ�����360��ıȼ��㣮
��� �⣺��1����Ƶ���ֲ�����֪����Ħ�г���Ƶ����24��Ƶ����0.2��
����������Ϊ24��0.2=120��
�ʴ�Ϊ��120��
��2��m=120��0.25=30��
n=36��120=0.3��
�ʴ�Ϊ��30��0.3��
��3����Ħ�г������ڵ����ε�Բ�ĽǵĶ���Ϊ��0.3��360��=108�㣬
�𣺡�Ħ�г������ڵ����ε�Բ�ĽǵĶ���Ϊ108�㣮
���� ���⿼���������ͼ��Ƶ���ֲ���������ͼ��֪ʶ������ͳ��ͼ����ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����y��Գ� | B�� | ����x��Գ� | ||
| C�� | ���������ᶼ�Գ� | D�� | ���ϴ𰸶��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
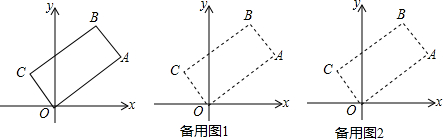
 ��ͼ���ı���ABCD��ƽ���ı��Σ�
��ͼ���ı���ABCD��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
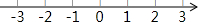 �ⲻ��ʽ�飺$\left\{\begin{array}{l}{1+x��-2��}&{��}\\{\frac{2x-1}{3}��1��}&{��}\end{array}\right.$������������գ���ɱ���Ľ��
�ⲻ��ʽ�飺$\left\{\begin{array}{l}{1+x��-2��}&{��}\\{\frac{2x-1}{3}��1��}&{��}\end{array}\right.$������������գ���ɱ���Ľ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
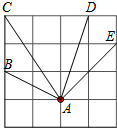 ��ͼ����4��4������ͼ�У�С�����εı߳�Ϊ1����ͼ������ĸ��ʾ�������߶��г���Ϊ$\sqrt{10}$���߶���AD��
��ͼ����4��4������ͼ�У�С�����εı߳�Ϊ1����ͼ������ĸ��ʾ�������߶��г���Ϊ$\sqrt{10}$���߶���AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��a��b�������dzߵ�ֱ�Ƕ������ֱ��b�ϣ���1=35�㣬���2�Ķ�����
��ͼ��ֱ��a��b�������dzߵ�ֱ�Ƕ������ֱ��b�ϣ���1=35�㣬���2�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com