
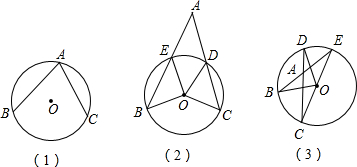
分析 (1)连接AO并延长交⊙O于M,连接BO,CO,由OA=OB=OC,得到∠1=∠B,∠2=∠C,根据角平分线的定义得到∠BOM=$\frac{1}{2}$∠1,∠COM=$\frac{1}{2}∠$2,于是得到结论;
(2)如图2,连接OA,根据三角形的外角的性质得到∠BOC=∠B+∠BAC+∠C,由于∠B=∠BEO=∠EAO+∠EOA,∠C=∠ODC=∠AOD+∠OAD,于是得到∠BOC=∠EOD+2∠BAC,即可得到结果;
(3)根据三角形的外角的性质得到∠BOC=2∠E,∠BAC=∠E+∠C,∠DOE=2∠C,于是推出∠BAC=2∠E+2∠C,即可得到结论.
解答 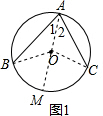 解:(1)连接AO并延长交⊙O于M,连接BO,CO,
解:(1)连接AO并延长交⊙O于M,连接BO,CO,
∵OA=OB=OC,
∴∠1=∠B,∠2=∠C,
∴∠BOM=$\frac{1}{2}$∠1,∠COM=$\frac{1}{2}∠$2,
∴∠BAC=$\frac{1}{2}∠$BOC;
(2)如图2,连接OA,
∴∠BOC=∠B+∠BAC+∠C,
∵∠B=∠BEO=∠EAO+∠EOA,∠C=∠ODC=∠AOD+∠OAD,
∴∠BOC=∠EOD+2∠BAC,
∴∠BOC-∠EOD=2∠BAC;
(3)2∠BAC=∠BOC+∠DOE,
理由:∵∠BOC=2∠E,∠BAC=∠E+∠C,∠DOE=2∠C,
∴∠BAC=∠E+∠C=$\frac{1}{2}∠$BOC+$\frac{1}{2}∠$DOE=$\frac{1}{2}$(∠BOC+∠DOE),
∴2∠BAC=∠BOC+∠DOE.
点评 本题考查了圆周角定理,三角形的内角和,三角形的外角的性质,熟练掌握各性质定理是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | b≤-6 | B. | b≤-5 | C. | b≥0 | D. | b≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
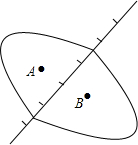 如图是王先生祖居的位置图,由于保存不慎已残缺不全,但可知钟楼的坐标为A(5,-2),街口坐标为B(5,2),资料记载王先生祖居的老屋坐标为(1,1),你能帮王先生找到祖居的老屋吗?
如图是王先生祖居的位置图,由于保存不慎已残缺不全,但可知钟楼的坐标为A(5,-2),街口坐标为B(5,2),资料记载王先生祖居的老屋坐标为(1,1),你能帮王先生找到祖居的老屋吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com