
【题目】已知代数式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.
(1)求c的值;
(2)已知当x=1时,该代数式的值为﹣1,试求a+b+c的值;
(3)已知当x=3时,该代数式的值为9,试求当x=﹣3时该代数式的值;
(4)在第(3)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小?
【答案】
(1)解:把x=0代入代数式,得到ax5+bx3+3x+c=c=﹣1;
∴c=﹣1
(2)解:把x=1代入代数式,得到ax5+bx3+3x+c=a+b+3+c=﹣1,
∴a+b+c=﹣4
(3)解:把x=3代入代数式,得到ax5+bx3+3x+c=35a+33b+3×3+c=9,
∴35a+33b+c=0;35a+33b=﹣c=1,
当x=﹣3时,原式=(﹣3)5a+(﹣3)3b+3×(﹣3)+c=﹣(35a+33b)﹣9+c=c﹣9+c=2c﹣9=﹣2﹣9=﹣11
(4)解:由(3)题得35a+33b=1,即9a+b= ![]() ,
,
又∵3a=5b,所以15b+b= ![]()
∴b= ![]() >0;
>0;
则a= ![]() b>0;
b>0;
∴a+b>0;
∵c=﹣1<0,
∴a+b>c
【解析】(1)把x=0代入代数式即可求出c的值;(2)把x=1代入代数式可求a+b=c的值;(3)把x=3代入代数式,再把得到的式子整体代入代数式,即可求值;(4)利用35a+33b=﹣9,再结合3a=5b,可求出a、b的值,从而可比较a+b与c的大小.


科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生的课余生活情况,学校决定围绕“在欣赏音乐、读课外书、体育运动、其他活动中,你最喜欢的课余生活种类是什么?(只写一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢欣赏音乐的学生占被抽取人数的12%,请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)最喜欢读课外书的学生占被抽取人数的百分数是多少?
(3)如果全校有1 000名学生,请你估计全校最喜欢体育运动的学生约有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC边长为6,AD是△ABC的中线,P为线段AD(不包括端点A、D)上一动点,以CP为一边且在CP左下方作如图所示的等边△CPE,连结BE. 
(1)点P在运动过程中,线段BE与AP始终相等吗?说说你的理由;
(2)若延长BE至F,使得CF=CE=5,如图2,问: ①求出此时AP的长;
②当点P在线段AD的延长线上时,判断EF的长是否为定值,若是请直接写出EF的长;若不是请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( ) 
A.P为∠A,∠B两角平分线的交点
B.P为AC,AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为AC,AB两边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3). 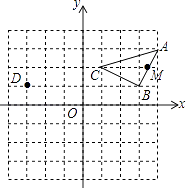
(1)点B和点C的坐标分别是、 .
(2)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF.
并直接写出E、F的坐标.
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季是流行性感冒高发的季节.某种感冒病毒的直径是0.00000002019米,数据0.00000002019用科学记数法可表示为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com