
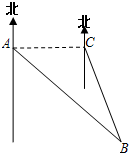
 (2013•徐汇区一模)如图,小岛B正好在深水港口A的东南方向,一艘集装箱货船从港口A出发,沿正东方向以每小时30千米的速度行驶,40分钟后在C处测得小岛B在它的南偏东15°方向,求小岛B离开深水港口A的距离.(精确到0.1千米)
(2013•徐汇区一模)如图,小岛B正好在深水港口A的东南方向,一艘集装箱货船从港口A出发,沿正东方向以每小时30千米的速度行驶,40分钟后在C处测得小岛B在它的南偏东15°方向,求小岛B离开深水港口A的距离.(精确到0.1千米)| 2 |
| 6 |
 解:由题意,得AC=30×
解:由题意,得AC=30×| 2 |
| 3 |
| 2 |
| 2 |
| 6 |
| 2 |
| 6 |
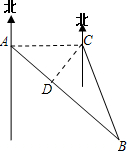
 [方法二]过点B作BD⊥AC,交AC延长线于D. …(1分)
[方法二]过点B作BD⊥AC,交AC延长线于D. …(1分)| 20 |
| 0.73 |
| 2 |
| 2 |
| 20 |
| 0.73 |
| 20 |
| 0.73 |


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
 (2013•徐汇区一模)“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究.得出结论:如图1,在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,如果∠A=2∠B,那么a2-b2=bc.
(2013•徐汇区一模)“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究.得出结论:如图1,在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,如果∠A=2∠B,那么a2-b2=bc.| BC |
| CD |
| AC |
| BC |
| a |
| b+c |
| b |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 | 5 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com