

分析 (1)过点C作CM∥AB交AG的延长线于M,如图1,利用等边三角形的性质得∠BAC=∠ACB=60°,AC=BC,则利用平行线的性质得∠DAF=∠M,∠AFD=∠CFM,∠ACM=120°,接着证明△ADF≌△MCF得到AD=MC,则AD=CE=CM,然后证明△BCE≌△ACM得到∠2=∠1,再利用三角形外角性质计算出∠AGB的度数;
(2)作DN∥CH交AG于N,如图2,先证明△DNF≌△CHF得到NF=HF,DN=CH,设HF=x,则CH=2HF=2x,NH=DN=2x,在判定点A、B、G、C四点共圆,则根据圆内接四边形的性质得∠AGC=∠ABC=60°,接着证明△CGH为等边三角形得到HG=CH=CG=2x,然后理由平分线分线段成比例定理,由DN∥BG得到$\frac{DN}{BG}$=$\frac{AN}{AG}$,即$\frac{2x}{BG}$=$\frac{AG-4x}{AG}$①,接下来理由旋转的定义,可把△CBG绕点C顺时针旋转60°可得到△CAH,
所以BG=AH,则AG=BG+2x,即2x=AG-BG②,最后把②代入①得AG和BG的关系.
解答 (1)证明:过点C作CM∥AB交AG的延长线于M,如图1,
∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,AC=BC,
∵AD∥CM,
∴∠DAF=∠M,∠AFD=∠CFM,∠ACM=120°,
∵点F为CD的中点,
∴DF=CF,
在△ADF和△MCF
$\left\{\begin{array}{l}{∠DAF=∠M}\\{∠DFA=∠CFM}\\{DF=CF}\end{array}\right.$,
∴△ADF≌△MCF,
∴AD=MC,
∵AD=CE,
∴CM=CE,
在△BCE和△ACM中
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACM}\\{CE=CM}\end{array}\right.$,
∴△BCE≌△ACM,
∴∠2=∠1,
∵∠ACB=∠2+∠E=60°,
∴∠AGB=∠1+∠E═∠2+∠E=60°;
(2)解:AG=$\sqrt{2}$BG.理由如下:
作DN∥CH交AG于N,如图2,
∵CH∥DN,
∴∠NDF=∠HCF,
在△DNF和△CHF中
$\left\{\begin{array}{l}{∠NDF=∠HCF}\\{DF=CF}\\{∠DFN=∠CFH}\end{array}\right.$,
∴△DNF≌△CHF,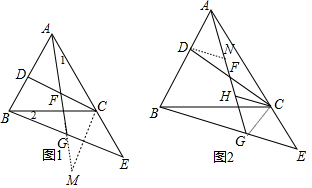
∴NF=HF,DN=CH,
设HF=x,则CH=2HF=2x,NH=DN=2x,
∵∠AGB=60°,∠ACB=60°,
∴点A、B、G、C四点共圆,
∴∠AGC=∠ABC=60°,
∵CH∥BE,
∴∠CHG=∠BGH=60°,
∴△CGH为等边三角形,
∴HG=CH=CG=2x,
∵DN∥BG,
∴$\frac{DN}{BG}$=$\frac{AN}{AG}$,即$\frac{2x}{BG}$=$\frac{AG-4x}{AG}$①,
∵∠ACB=∠GCH=60°,CH=CG,CB=CA,
∴将△CBG绕点C顺时针旋转60°可得到△CAH,
∴BG=AH,
∴AG=AH+HG=BG+2x,
∴2x=AG-BG②,
把②代入①得$\frac{AG-BG}{BG}$=$\frac{AG-2(AG-BG)}{AG}$,
整理得AG2=2BG2,
∴AG=$\sqrt{2}$BG.
点评 本题考查了四点共圆:熟练掌握四点共圆的判定方法、圆内接四边形的性质、旋转的性质和等边三角形的性质;灵活运用三角形全等的知识证明线段或角相等;充分运用中点构建全等三角形;会运用相似比建立线段之间的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | a≥b | C. | a<b | D. | a≤b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
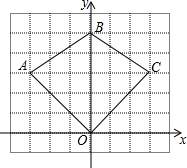 如图△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:
如图△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD∥BC,CE⊥AB,△BDC为等腰直角三角形,∠BDC=90°,BD=CD;CE与BD交于F,连AF,M为BC中点,连接DM交CE于N.请说明:
如图,四边形ABCD中,AD∥BC,CE⊥AB,△BDC为等腰直角三角形,∠BDC=90°,BD=CD;CE与BD交于F,连AF,M为BC中点,连接DM交CE于N.请说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
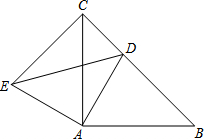 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com