
 中,
中, ,
, .点
.点 ,
, ,
,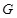 分别在边
分别在边 ,
, ,
, 上,
上, .
.
 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形 是矩形.
是矩形.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明; ∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.
∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.6 cm和9 cm | B.5 cm和10 cm | C.4 cm和11 cm | D.7 cm和8 cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.顺次连结菱形各边中点所得的四边形是矩形 |
| B.有一个角是直角的菱形是正方形 |
| C.对角线相等且垂直的四边形是正方形 |
| D.有一个角是60°的等腰三角形是等边三角形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 =____________.
=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com