练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

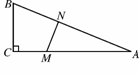
    如图6­4­23，在△ABC中，∠C＝90°，BC＝5米，AC＝12米．点M在线段CA上，从C向A运动，速度为1米/秒；同时点N在线段AB上，从A向B运动，速度为2米/秒，运动时间为t秒．

    (1)当t为何值时，∠AMN＝∠ANM；

    (2)当t为何值时，△AMN的面积最大？并求出这个最大值．


    解：(1)由题意，得AM＝12－t，AN＝2t.

    ∵∠AMN＝∠ANM，

    ∴AM＝AN，从而12－t＝2t，

    解得t＝4秒．

    ∴当t为4秒时，∠AMN＝∠ANM.

    (2)如图56，过点N作NH⊥AC于点H，

    ∴∠NHA＝∠C＝90°.

    ∵∠A是公共角，∴△NHA∽△BCA.

    ∴＝，即＝，∴NH＝.

    从而有S△AMN＝(12－t)·＝－t2＋t，

    ∴当t＝6时，S有最大值为.

       

    图56     　　　　图57


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


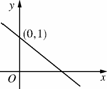
    如图3­2­11，一次函数y＝kx＋b的图象与y轴交于点(0,1)，则关于x的不等式kx＋b＞1的解集是(　　)

    A．x＞0　　  B．x＜0　　  C．x＞1　  D．x＜1

       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


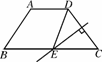
    如图4­3­59，在梯形ABCD中，AD∥BC，AD＝3，AB＝5，BC＝9，CD的垂直平分线交BC于点E，连接DE，则四边形ABED的周长等于(　　)

    A．17  B．18  C．19  D．20

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列各组线段(单位：cm)中，是成比例线段的为(　　)

    A．1,2,3,4  B．1,2,2,4  C．3,5,9,13  D．1,2,2,3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图6­4­18, 在▱ABCD，E在AB上，CE，DB交于F，若AE∶BE＝4∶3，且BF＝2，则DF＝________.

       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图6­1­16，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为(　　)

    A．6  B．8  C．10  D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


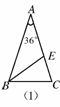
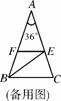
    如图6­1­23(1)，在△ABC中，∠A＝36°，AB＝AC，∠ABC的平分线BE交AC于E.

    (1)求证：AE＝BC；

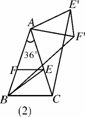
    (2)如图6­1­23(2)，过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α(0°＜α＜144°)得到△AE′F′，连接CE′，BF′，求证：CE′＝BF′；

    (3)在(2)的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．

    　　　　　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：O为直线AB上的一点，OC⊥OE于点O，射线OF平分∠AOE.

    (1)如图4­1­23(1)，判断∠COF和∠BOE之间的数量关系？并说明理由；

    (2)若将∠COE绕点O旋转至图4­1­23(2)的位置，试问(1)中∠COF和∠BOE之间的数量关系是否发生变化？若不发生变化，请你加以证明，若发生变化，请你说明理由；

    (3)若将∠COE绕点O旋转至图4­1­23(3)的位置，继续探究∠COF和∠BOE之间的数量关系，并加以证明．

      

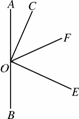
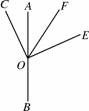
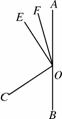
    (1)　　         (2)　        　 (3)

    图4­1­23

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，，则                ．

    查看答案和解析>>

    同步练习册答案