
【题目】小明早晨跑步,他从自家向东跑了2千米到达小彬家,继续向东跑了1.5千米到达小红家,然后向西跑了4.5千米到达中心广场,最后回到家.
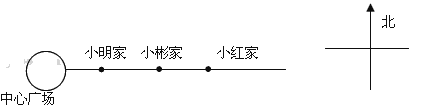
(1)以小明家为原点,以向东的方向为正方向,用1 个单位长度表示1千米,你能在数轴上表示出中心广场,小彬家和小红家的位置吗?
(2)小彬家距中心广场多远?
(3)小明一共跑了多少千米?
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,是因式分解的是( )
A. m2-1=(m+1)(m-1) B. 2(a-b)=2a-2b C. x2-2x+1=x(x-2)+1, D. a(a-b)(b+1)=(a2 -ab)(b+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证: 
(1)AF=CG;
(2)CF=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题中真命题是( )
①三角形有且只有一个内切圆;
②四边形的内角和与外角和相等;
③顺次连接四边形各边中点所得的四边形一定是菱形;
④一组对边平行且一组对角相等的四边形是平行四边形.
A.①②
B.③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
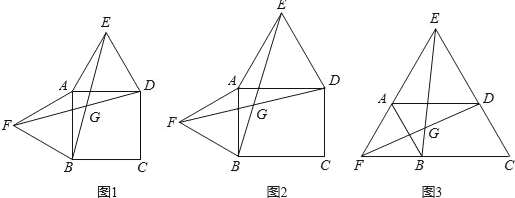
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.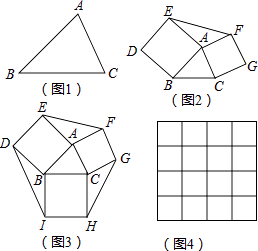
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为 . (提示:可先利用图4求出△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
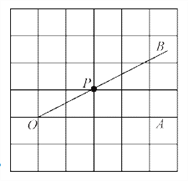
【题目】如图,在![]() 的正方形网格中,点P是
的正方形网格中,点P是![]() 的边OB上的一点.
的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com