����⣺��1����������y=x
2+px+q�У�
��x=0ʱ��y=q������C�������Ϊ��0��q����
��Ϊ��OA=OC��D����A�����y��Գƣ�
���ԣ�A�������Ϊ��q��0����D�������Ϊ��-q��0����
��A��q��0������y=x
2+px+q�еã�0=q
2+pq+q
����q��q+p+1��=0
���ԣ�q=0�������������⣬��ȥ����
q+p=-1 ��
�������P�����꣬��������y=x
2+px+q��������꣺
�����꣺-
�������꣺
��
��ֱ��CD�ķ���Ϊy=kx+b
��Ϊֱ��CD��C��0��q����D��-q��0�����㣬�����з�����
q=b��0=-qk+b��
��ã�k=1��b=q��
����ֱ��CD�Ľ���ʽΪ��y=x+q��
��Ϊ��P��ֱ��CD�ϣ�
����
=-
+q
��ã�p=0�����������⣬��ȥ��
p=2 ��
���Ѿ���õĢ١�������ʽ�ã�p=2��q=-3��
��ˣ�p��q��ֵ�ֱ�Ϊ 2��-3��
��2����p=2��q=-3��
�������ߵĽ���ʽΪy=x
2+2x-3��
A��D��C��P�ĵ������ֱ�Ϊ��-3��0������3��0������0��-3������-1��-4����
ֱ��CD�ķ���ʽΪy=x-3��
�裺��A����ֱ��CDƽ�е�ֱ��AQ�ķ���Ϊ��
y=x+b������ֱ��ƽ�У�����һ����ϵ����ȣ�
��Ϊ��A��-3��0����ֱ��AQ�ϣ��������y=x+b�еã�0=-3+b����ã�b=3
���ԣ�ֱ��AQ�ķ���Ϊ��y=x+3
������ֱ��AQ��y=x+3����������y=x
2+2x-3�Ľ���Q�����꣺
�ⷽ����y=x
2+2x-3��y=x+3����x
1=2��y
1=5��x
2=-3��y
2=0��
����������ΪA��-3��0����Q��2��5����
��������A��Q��������P��D������룺��ͼ�ο�֪
|AQ|=5
��|PD|=4
��
����|AQ|��|PD|
��˵��AQ��PD����ȣ��������������ϲ����������ı���APDQ��ƽ���ı��ε�Q�㣮
��3������E�㣬��E������Ϊ��9��6����
�������������£�
��E����ֱ��PC�ϵĵ㣬������AE��ֱAP
��ֱ��AP�ķ��̣���ֱ��AP�ķ���Ϊy=kx+b
��ΪA��-3��0����P��-1��-4��������ֱ��AP�ϣ������з�����
0=-3k+b��-4=-k+b����ã�k=-2��b=-6��
����ֱ��AP�ķ���ʽΪ��y=-2x-6
��Ϊֱ��AE��ֱֱ��AC��������ֱ��һ����ϵ��֮������-1
���ԣ���ֱ��AE����ʽΪy=
x+b
A��-3��0������ֱ��AE�ϣ�����b=
��
����ֱ��AE�ķ���ʽΪy=
x+
��
ֱ��AE��ֱ��CD�ཻ��E�㣬����ֱ�߷�����ɵķ�����ã�x=9��y=6��
��E���������9��6����
��������ACD�У���ΪOA=OD=OC��AD��ֱCO��
���ԡ�ACD��ֱ�ǣ�
��ֱ��������APE�У�AC��б��PE�ϵĸߣ�
���ԡ�APC�ס�EPA��

 ��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�
��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�

 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
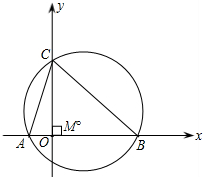 ��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M��
��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��1-
��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��1- ��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0����
��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0����