
请判断
(1)连结三角形式顶点和它的对边中点的线,叫做三角形的中线.
( )
(2)AM是△ABC的中线,则BM=CM.
( )
(3)钝角三角形和直角三角形只有一条高.
( )
(4)角的平分线和三角形的角平分线没有区别.
( )
(5)三角形的三条角平分线都在三角形的内部.
( )
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源:2009年浙江省金华市中考数学试题及答案(纯word版) 题型:044
在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连结OA,平移线段OA,使点O落在点B.设点A落在点C,作如下探究:
探究一:若点B的坐标为(1,2),请在图1中作出平移后的像,则点C的坐标是________;连结AC,BO,请判断O,A,C,B四点构成的图形的形状,并说明理由;
探究二:若点B的坐标为(6,2),按探究一的方法,判断O,A,B,C四点构成的图形的形状.
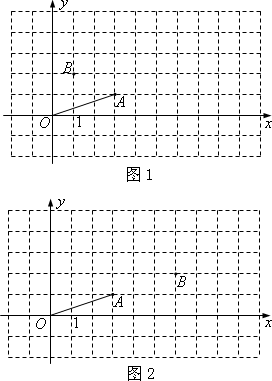
(温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!)
(2)通过上面的探究,请直接回答下列问题:
①若已知三点A(a,b),B(c,d),C(a+c,b+d),顺次连结O,A,C,B,请判断所得到的图形的形状;
②在①的条件下,如果所得到的图形是菱形或者是正方形,请选择一种情况,写出a,b,c,d应满足的关系式.
查看答案和解析>>
科目:初中数学 来源:2013届湖北宜城九年级上学期期中考试数学试卷(有解析) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北宜城九年级上学期期中考试数学试卷(有解析) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
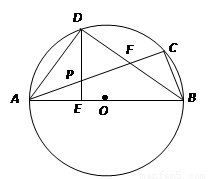
(1)求证:AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连结OA,平移线段OA,使点O落在点B.设点A落在点C,作如下探究:
探究一:若点B的坐标为(1,2),请在图1中作出平移后的像,则点C的坐标是 ▲ ;连结AC,BO,请判断O,A,C,B四点构成的图形的形状,并说明理由;

探究二:若点B的坐标为(6,2),按探究一的方法,判断O,A,B,C四点构成的图形的形状.
(2)通过上面的探究,请直接回答下列问题:
①若已知三点A (a,b),B(c,d),C (a+c,b+d),顺次连结O,A,C,B,请判断所得到的图形的形状;
②在①的条件下,如果所得到的图形是菱形或者是正方形,请选择一种情况,写出a,b,c,d应满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com