
请完成下面的说明:
【小题1】如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°-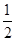 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=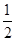 (∠EBC+∠FCB)=
(∠EBC+∠FCB)=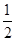 (180°+∠_____)=90°+
(180°+∠_____)=90°+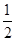 ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
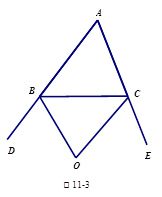
【小题2】如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+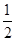 ∠A.
∠A.
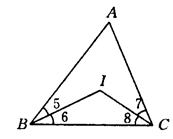
【小题3】用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?(直接写出结论)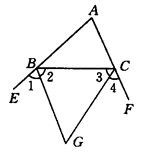
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
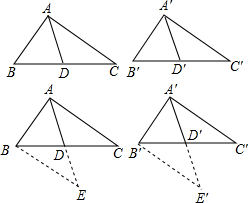 (2013•莒南县一模)【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(无需证明)
(2013•莒南县一模)【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(无需证明)查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
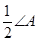 ,理由如下:
,理由如下: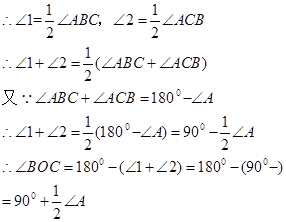


查看答案和解析>>
科目:初中数学 来源: 题型:
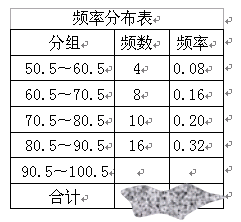

查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠_____)=90°+
(180°+∠_____)=90°+ ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____ ∠A.
∠A.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com