Question

7．已知两个全等的直角三角板ABC，DEF（如图1）放置，点B、D重合，点F在BC上，AB与EF交于点G，∠C=∠EFD=90°，∠E=∠ABC=30°，AB=DE=2．
（1）求证：△EGB是等腰三角形；
（2）若△ABC不动，问△DEF绕点F顺时针最少旋转多少度时，四边形ACDE成为以DE为底的梯形？（如图2）并求此梯形的高．

Answer 1

分析 （1）根据题意，即可发现∠EBG=∠E=30°，从而证明结论；
（2）要使四边形ACDE成为以ED为底的梯形，则需BC⊥DE，即可求得∠BFD=30°．再根据30°的直角三角形的性质即可求解．

解答 解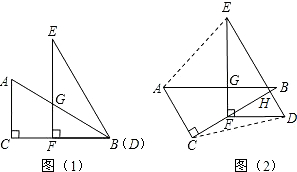：（1）证明：∵∠C=∠EFB=90°，∠E=∠ABC=30°，
∴∠EBF=60°，
∴∠EBG=∠EBF-∠ABC=60°-30°=∠E．
∴GE=GB，
则△EGB是等腰三角形；

（2）解：要使四边形ACDE成为以ED为底的梯形，
则需BC⊥DE，即可求得∠BFD=30°．
∴△DEF绕点F顺时针最少旋转多少度时，四边形ACDE成为以DE为底的梯形．
设BC与DE的交点是H．
在直角三角形DFE中，∠FDH=60°，DF=$\frac{1}{2}$DE=1，
在直角三角形DFH中，FH=DF•cos∠BFD=1×cos30°=$\frac{\sqrt{3}}{2}$，
则CH=BC-BH=AB•cos∠ABC-（BF-FH）=$\sqrt{3}$-（1-$\frac{\sqrt{3}}{2}$）=$\frac{3\sqrt{3}}{2}$-2．
即此梯形的高是$\frac{3\sqrt{3}}{2}$-2．
故答案为：$\frac{3\sqrt{3}}{2}$-2．

点评 此题是三角形综合题，主要考查了含30°的直角三角形的性质，锐角三角函数，等腰三角形的判定，梯形的性质，旋转的性质，解本题的关键是求出DF．