
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F。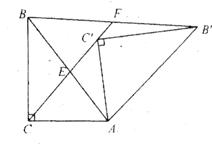
(1)若AC=3,AB=4,求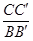
(2)证明:△ACE∽△FBE;
(3)设∠ABC=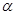 ,∠CAC′=
,∠CAC′=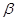 ,试探索
,试探索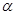 、
、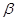 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
(1) (2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
(2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
∴△ACE∽△FBE(3)
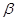 =
=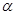 时△ACE≌△FBE。
时△ACE≌△FBE。
解析试题分析:解(1)∵Rt△AB′C′是由Rt△ABC绕点A旋转得到的
∴AC=AC′,∠CAC′=∠BAB′,AB=AB′,∴
∴△CAC′∽△BAB′,∴
(2)由(1)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
∴△ACE∽△FBE
(3)当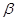 =2
=2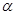 时,△ACE与△FBE全等
时,△ACE与△FBE全等
由(1)可知△CAC′是等腰三角形,∠ACC′=
∴∠BCE=90°-∠ACC′=
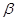 =
=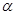 ,∠ABC=
,∠ABC=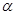 ,∴∠BCE=∠ABC
,∴∠BCE=∠ABC
∴BE=CE,又△ACE∽△FBE,∴△ACE≌△FBE
考点:相似三角形与全等三角形判定
点评:本题难度中等,主要考查学生对相似三角形性质与全等三角形判定等知识点的掌握与运用能力,为中考常考题型,要注意数形结合应用。


科目:初中数学 来源: 题型:
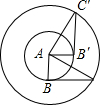 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中弧CC′的长为( )
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中弧CC′的长为( )A、
| ||||
B、
| ||||
| C、5π | ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明:
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
| CC′ | BB′ |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com