解:(1)∵△ABC,△DBE为等腰直角三角形,
∴AC∥DE,
∵M,N为DC,DE中点,
∴MN∥CE,
∴MN∥BC,
同理可证:FG∥BC,FM∥AB,GN∥AB,
∴FGNM为平行四边形,
又∵AB⊥BC,
∴GN⊥MN,
∴FGNM为矩形,
∴AD=CE,MN=

CE,
∴MN=

CE=

AD=GN,
∴FGNM为正方形;
(2)∵F,M,N,G分别为线段AC,CD,ED,AE的中点,
∴FG,FM,MN,NG分别为△ACE,△ACD,△DCE,△AED的中位线.
∴FG=MN=

•CE,FM=NG=

•AD,
∴四边形FMNG是平行四边形;
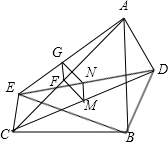
分析:(1)根据已知条件得出AC∥DE,MN∥CE,MN∥BC,FG∥BC,FM∥AB,GN∥AB,即可得出FGNM为平行四边形,再根据AB⊥BC,得出GN⊥MN,从而得出FGNM为矩形,最后根据中位线的性质得出MN=

CE=

AD=GN,即可得出四边形FMNG的形状;
(2))根据F,M,N,G分别为线段AC,CD,ED,AE的中点,得出FG,FM,MN,NG分别为△ACE,△ACD,△DCE,△AED的中位线,从而证出四边形FMNG是平行四边形;
点评:此题考查了三角形中位线定理,用到的知识点是全等三角形的判定与性质、等腰直角三角形、中位线等,解题的关键是根据中位线的性质进行解答.

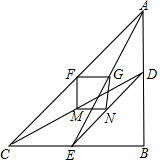 两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点.
两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点. CE,
CE, CE=
CE= AD=GN,
AD=GN, •CE,FM=NG=
•CE,FM=NG= •AD,
•AD,
 CE=
CE= AD=GN,即可得出四边形FMNG的形状;
AD=GN,即可得出四边形FMNG的形状;

 名校课堂系列答案
名校课堂系列答案