【题目】某厂准备购买
、
、
三种配件共
件，要求购买时
配件的件数是
配件数的
倍， 
配件不超过
件，且每种配件都必须买，三种配件的价格如下： 
、
、
三种配件的单价分别为
元、
元、
元．
（
）求购买
配件的件数范围．
（
）三种配件应各买多少件，才能使买配件的总费用最少？总费用最少多少元？
【答案】（1）
；（2）
配件买
件， 
配件买
件， 
配件买
件，所需总费用最少
元．
【解析】试题分析：（1）设买A种配件x件，B种配件（1000-5x）件，C种配件4x件，根据B配件不超过400件列出不等式组，解不等式组即可得x的取值范围；（2）设总费用为y元，根据题意列出y与x的函数关系式，根据x的取值范围和一次函数的性质可得即可解决问题.
试题解析：
（1）设买A种配件x件，B种配件（1000-5x）件，C种配件4x件，因为B配件不超过400件，所以0<1000-5x≤400，即可得120≤x<200．
（2）设总费用为y元，根据题意得：y=30x+(1000-5x)×50+80×40x=100x+50000(120≤x<200)．
当x=120时，y最小，y=100×120+50000=62000（元），1000-5x=400，4x=480．
答： A配件买120件，B配件买400件，C配件买480件，所需总费用最少为62000元．
快捷英语周周练系列答案科目：初中数学 来源： 题型：
【题目】如图，在¨ABCD中，过点D作DE⊥AB与点E，点F在边CD上，DF=BE,连接AF,BF
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB.
查看答案和解析>>
科目：初中数学 来源： 题型：
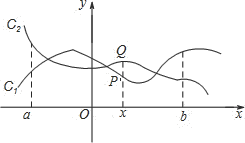
【题目】如图，点
与
分别是两个函数图象
与
上的任一点．当
时，有
成立，则称这两个函数在
上是“相邻函数”，否则称它们在
上是“非相邻函数”．例如，点
与
分别是两个函数
与
图象上的任一点，当
时， 
，通过构造函数
并研究它在
上的性质，得到该函数值得范围是
，所以
成立，因此这两个函数在
上是“相邻函数”．
（
）判断函数
与
在
上是否为“相邻函数”，并说明理由．
（
）若函数
与
在
上是“相邻函数”，求
的取值范围．
（
）若函数
与
在
上是“相邻函数”，直接写出
的最大值与最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用数学的方式理解“当窗理云鬓，对镜贴花黄”和“坐地日行八万里”（只考虑地球的自转），其中蕴含的图形运动是（ ）
A.平移和旋转
B.对称和旋转
C.对称和平移
D.旋转和平移
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置．设BC=2，AC=2
，则顶点A运动到点A″的位置时，点A经过的路线与直线l所围成的面积是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com