
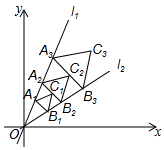
 ��ͼ����A1��1��$\sqrt{3}}$����ֱ��l1��y=$\sqrt{3}$x�ϣ�����A1��A1B1��l1��ֱ��l2��y=$\frac{{\sqrt{3}}}{3}$x�ڵ�B1����A1B1Ϊ���ڡ�OA1B1������ȱ�������A1B1C1���ٹ���C1��A2B2��l1���ֱ�ֱ��l1��l2��A2��B2���㣬��A2B2Ϊ���ڡ�OA2B2������ȱ�������A2B2C2�������˹��ɽ�����ȥ�����n���ȱ�������AnBnCn�����Ϊ$\frac{\sqrt{3}}{2}$$��\frac{3}{2}��^{2n-3}$�����ú�n�Ĵ���ʽ��ʾ��
��ͼ����A1��1��$\sqrt{3}}$����ֱ��l1��y=$\sqrt{3}$x�ϣ�����A1��A1B1��l1��ֱ��l2��y=$\frac{{\sqrt{3}}}{3}$x�ڵ�B1����A1B1Ϊ���ڡ�OA1B1������ȱ�������A1B1C1���ٹ���C1��A2B2��l1���ֱ�ֱ��l1��l2��A2��B2���㣬��A2B2Ϊ���ڡ�OA2B2������ȱ�������A2B2C2�������˹��ɽ�����ȥ�����n���ȱ�������AnBnCn�����Ϊ$\frac{\sqrt{3}}{2}$$��\frac{3}{2}��^{2n-3}$�����ú�n�Ĵ���ʽ��ʾ�� ���� �ɵ�A1������ɵó�OA1=2������ֱ��l1��l2�Ľ���ʽ��Ͻ�ֱ�������ο����A1B1�ij��ȣ��ɵȱ������ε����ʿɵó�A1A2�ij��ȣ������ó�OA2=3��ͨ����ֱ�������οɵó�A2B2�ij��ȣ�ͬ�������AnBn�ij��ȣ��ٸ��ݵȱ������ε������ʽ���������n���ȱ�������AnBnCn�������
��� �⣺�ߵ�A1��1��$\sqrt{3}}$����
��OA1=2��
��ֱ��l1��y=$\sqrt{3}$x��ֱ��l2��y=$\frac{{\sqrt{3}}}{3}$x��
���A1OB1=30�㣮
��Rt��OA1B1�У�OA1=2����A1OB1=30�㣬��OA1B1=90�㣬
��A1B1=$\frac{1}{2}$OB1��
��A1B1=$\frac{2\sqrt{3}}{3}$��
�ߡ�A1B1C1Ϊ�ȱ������Σ�
��A1A2=$\frac{\sqrt{3}}{2}$A1B1=1��
��OA2=3��A2B2=$\sqrt{3}$��
ͬ�����ɵó���A3B3=$\frac{3\sqrt{3}}{2}$��A4B4=$\frac{9\sqrt{3}}{4}$������AnBn=$��\frac{3}{2}��^{n-2}$$\sqrt{3}$��
���n���ȱ�������AnBnCn�����Ϊ$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$AnBn2=$\frac{\sqrt{3}}{2}$$��\frac{3}{2}��^{2n-3}$��
�ʴ�Ϊ��$\frac{\sqrt{3}}{2}$$��\frac{3}{2}��^{2n-3}$��
���� ���⿼����һ�κ���ͼ���ϵ��������������ֱ���������Լ��ȱ������ε����ʣ�ͨ����ֱ�������μ��ȱ������ε����ʣ��ҳ�AnBn=$��\frac{3}{2}��^{n-2}$$\sqrt{3}$�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
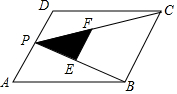 ��ͼ��PΪ?ABCD�ı�AD�ϵ�һ�㣬E��F�ֱ���PB��PC���е㣬��PEF����PDC����PAB������ֱ�ΪS��S1��S2����S=3����S1+S2��ֵ�ǣ�������
��ͼ��PΪ?ABCD�ı�AD�ϵ�һ�㣬E��F�ֱ���PB��PC���е㣬��PEF����PDC����PAB������ֱ�ΪS��S1��S2����S=3����S1+S2��ֵ�ǣ�������| A�� | 3 | B�� | 6 | C�� | 12 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��A��B������ֱ�Ϊ��0��1������3��0���������߶�ABƽ����A1B1����a+b��ֵΪ��������
��ͼ��A��B������ֱ�Ϊ��0��1������3��0���������߶�ABƽ����A1B1����a+b��ֵΪ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪�����ABCDE�ı߳�����ȣ��ҡ�DBE=��ABE+��CBD��AC=1����BD�ض����㣨������
��ͼ����֪�����ABCDE�ı߳�����ȣ��ҡ�DBE=��ABE+��CBD��AC=1����BD�ض����㣨������| A�� | BD��2 | B�� | BD=2 | ||
| C�� | BD��2 | D�� | ������������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com