
 cot260°+sin30°+tan36°-4tan45°cos45°-cot54°
cot260°+sin30°+tan36°-4tan45°cos45°-cot54°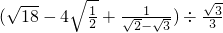
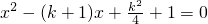 ,
, cot260°+sin30°+tan36°-4tan45°cos45°-cot54°
cot260°+sin30°+tan36°-4tan45°cos45°-cot54° ×
× +
+ +tan36°-4×1×
+tan36°-4×1× -cot54°
-cot54° +
+ -2
-2
 ;
;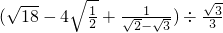
 -2
-2 -
- -
- )×
)×
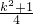 )≥0,
)≥0, ,
, 时,此方程有实数根;
时,此方程有实数根;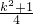 >0,
>0, .
. .
.

科目:初中数学 来源:2011-2012学年四川省资阳市安岳县自治乡九义校九年级(上)期末数学试卷(解析版) 题型:解答题
 cot260°+sin30°+tan36°-4tan45°cos45°-cot54°
cot260°+sin30°+tan36°-4tan45°cos45°-cot54°
 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com