Question

1．已知；如图1，△OAB是边长为2的等边三角形，OA在x轴上，点B在第一象限内，△OCA是一个等腰三角形，OC=AC，顶点C在第四象限，∠C=120°．现有两动点P、Q分别从A、O两点同时出发，点Q以每秒1个点位的速度沿OC向点C运动，点P以每秒3个单位的速度沿A→Q→B运动，当其中一个点到达终点时，另一个点也随即停止．
（1）OC=$\frac{2\sqrt{3}}{3}$；点C的坐标为（1，-$\frac{\sqrt{3}}{3}$），；
（2）求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系，并写出自变量t的取值范围；
（3）如图2，现有∠MCN=60°，其两边分别与OB、AB交于点M，N，连接MN，将∠MCN绕着C点旋转（0°＜旋转角＜60°），使得M、N始终在边OB和边AB上，试判断在这一过程中，△BMN的周长是否发生变化？若没有变化，请直接写出其周长；若发生变化，说明理由．

Answer 1

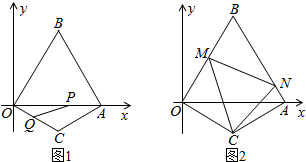
分析 （1）根据等边三角形的性质和坐标特点解答即可；
（2）由于点Q从点O运动到点C需要$\frac{2\sqrt{3}}{3}$秒，点P从点A→O→B需要$\frac{4}{3}$秒，所以分两种情况讨论：①0＜t＜$\frac{2}{3}$；②$\frac{2}{3}$≤t＜$\frac{2\sqrt{3}}{3}$．针对每一种情况，根据P点所在的位置，由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系，并且得出自变量t的取值范围；
（3）如果延长BA至点F，使AF=OM，连接CF，则由SAS可证△MOC≌△FAC，得出MC=CF，再由SAS证出△MCN≌△FCN，得出MN=NF，那么△BMN的周长=BA+BO=4．

解答 解：（1）因为OA=2，∠C=120°，OC=AC，
所以可得：$O{C}^{2}=（\frac{1}{2}OA）^{2}+（\frac{1}{2}OC）^{2}$，
解得：OC=$\frac{2\sqrt{3}}{3}$，
所以点C的坐标为（1，-$\frac{\sqrt{3}}{3}$），
故答案为：$\frac{2\sqrt{3}}{3}$；（1，-$\frac{\sqrt{3}}{3}$）；
（2）过点C作CD⊥OA于点D．（如图1）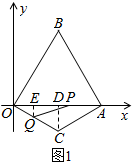
∵OC=AC，∠ACO=120°，
∴∠AOC=∠OAC=30°．
∵OC=AC，CD⊥OA，
∴OD=DA=1．
在Rt△ODC中，OC=$\frac{OD}{cos30°}=\frac{1}{cos30°}=\frac{2\sqrt{3}}{3}$；
（i）当0＜t＜$\frac{2}{3}$时，OQ=t，AP=3t，OP=OA-AP=2-3t．
过点Q作QE⊥OA于点E．（如图1）
在Rt△OEQ中，
∵∠AOC=30°，
∴QE=$\frac{1}{2}$OQ=$\frac{t}{2}$，
∴S_△OPQ=$\frac{1}{2}$OP•EQ=$\frac{1}{2}$（2-3t）•$\frac{t}{2}$=$-\frac{3}{4}{t}^{2}+\frac{1}{2}t$，
即S=$-\frac{3}{4}{t}^{2}+\frac{1}{2}t$；
（ii）当$\frac{2}{3}$＜t≤$\frac{2\sqrt{3}}{3}$时，（如图2）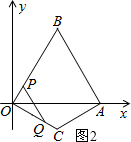

OQ=t，OP=3t-2．
∵∠BOA=60°，∠AOC=30°，
∴∠POQ=90°．
∴S_△OPQ=$\frac{1}{2}$OQ•OP=$\frac{1}{2}$t•（3t-2）=$\frac{3}{2}{t}^{2}$-t，
即S=$\frac{3}{2}{t}^{2}$-t；
故当0＜t＜$\frac{2}{3}$时，S=-$\frac{3}{4}{t}^{2}$+$\frac{1}{2}$t；当$\frac{2}{3}$＜t≤$\frac{2\sqrt{3}}{3}$时，S=$\frac{3}{2}{t}^{2}$-t．
（3）△BMN的周长不发生变化．理由如下：
延长BA至点F，使AF=OM，连接CF．（如图3）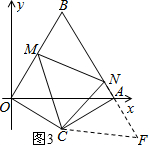

又∵∠MOC=∠FAC=90°，OC=AC，
∴△MOC≌△FAC，
∴MC=CF，∠MCO=∠FCA．
∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA
=∠OCA-∠MCN
=60°，
∴∠FCN=∠MCN．
在△MCN和△FCN中，
$\left\{\begin{array}{l}{MC=CF}\\{∠FCN=∠MCN}\\{CN=CN}\end{array}\right.$，
∴△MCN≌△FCN，
∴MN=NF．
∴BM+MN+BN=BM+NF+BN=BO-OM+BA+AF=BA+BO=4．
∴△BMN的周长不变，其周长为4．

点评 本题综合考查了等腰三角形、等边三角形的性质，全等三角形的判定．难度很大．注意分类讨论时，做到不重复，不遗漏．