
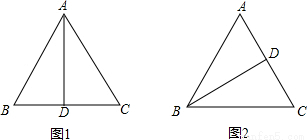
 解:如图,等腰三角形△ABC,AB=AC,面积为30m2
解:如图,等腰三角形△ABC,AB=AC,面积为30m2 AD×BC=30,
AD×BC=30, BC=5,
BC=5,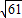 ,
, AC×BD=30,
AC×BD=30,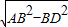 =8,
=8,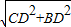 =2
=2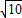 ,
,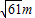 、
、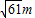 或10m、
或10m、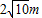 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(山东潍坊卷)数学(解析版) 题型:解答题
为了美化校园环境,建设绿色校园,某学校准备对校园中30亩空地进行绿化..绿化采用种植草皮与种植树木两种方式,要求种植草皮与种植树木的面积都不少于10亩,并且种植草皮面积不少于种植树木面积的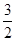 .已知种植草皮与种植树木每亩的费用分别为8000元与12000元.
.已知种植草皮与种植树木每亩的费用分别为8000元与12000元.
(1)种植草皮的最小面积是多少?
(2)种植草皮的面积为多少时绿化总费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com