解:(1)∵点A的坐标为(-2,m),
∴OB=2,AB=m,
∴
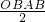
=2,即

=2,
∴m=2,
则点A的坐标为(-2,2),
把点A的坐标代入y=

中,得k=-4,
则反比例函数的解析式为:y=-

;
(2)将y=-1代入由(1)得出的反比例函数解析式y=-

中,得x=4,
可得C(4,-1),
又有A(-2,2),
将A和C坐标代入y=ax+b中,得
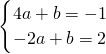
,
解得:
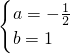
,
则直线解析式为y=-

x+1;
(3)在y轴上存在点P,使△AOP是等腰三角形,
分四种情况考虑,如图所示:
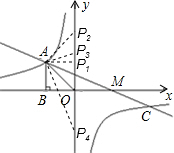
当AP
1=P
1O时,△AP
1O为等腰直角三角形,
∵A(-2,2)
,∴AP
1=OP
1=2,
此时P
1(0,2);
当OA=OP
3时,∵A(-2,2),
∴OA=2

,
此时P
3(0,2

);
当OA=AP
2时,OP
2=4,
此时P
2(0,4);
当OA=OP
4时,由OA=2

,得到OP
4=2

,
此时P
4(0,-2

).
综上,满足题意坐标为P
1(0,2),P
2(0,4),P
3(0,2

),P
4(0,-2

).
分析:(1)由A的坐标表示出AB及OB的长,根据直角三角形的面积等于两直角边乘积的一半,由AB与BO乘积的一半表示出三角形AOB的面积,根据三角形AOB的面积为2列出关于m的方程,求出方程的解得到m的值,确定出A的坐标,将A的坐标代入反比例函数解析式中,求出k的值,即可确定出反比例函数解析式;
(2)由A和C两点在反比例函数图象上,将C的坐标代入反比例函数解析式中,求出n的值,确定出C的坐标,然后将A和C的坐标代入y=ax+b中,得到关于a与b的二元一次方程组,求出方程组的解集得到a与b的值,即可确定出一次函数y=ax+b的解析式;
(3)在y轴上存在点P,使△AOP是等腰三角形,分四种情况考虑:当AP
1=P
1O时;当OA=OP
3时;当OA=AP
2时;当OA=OP
4时,分别根据A的坐标得出OA的长,即可确定出各种情况P的坐标.
点评:本题考查了反比例函数与一次函数的交点,及待定系数法求函数解析式,利用了数形结合及分类讨论的思想,难度较大,解题的关键是掌握用待定系数法求函数解析式,同时第三问满足题意的点P坐标要找对、找全.

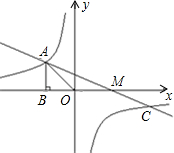 已知反比例函数
已知反比例函数 的图象过第二象限的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为2,若直线y=ax+b经过点A,并且经过反比例函数
的图象过第二象限的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为2,若直线y=ax+b经过点A,并且经过反比例函数 的图象上另一点C(n,-1).
的图象上另一点C(n,-1).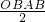 =2,即
=2,即 =2,
=2, 中,得k=-4,
中,得k=-4, ;
; 中,得x=4,
中,得x=4,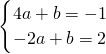 ,
,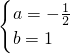 ,
, x+1;
x+1;
 ,
, );
); ,得到OP4=2
,得到OP4=2 ,
, ).
). ),P4(0,-2
),P4(0,-2 ).
).
