
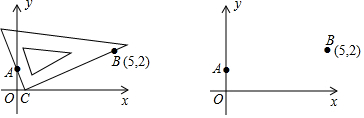
���� ��1�����ݡ����IJ����IJ�������������D���ɣ�
��2������B��BD��x���ڵ�D�����ݡ�AOC�ס�CDB���ɵ�$\frac{AO}{CD}$=$\frac{OC}{BD}$�������ó�$\frac{1}{5-m}$=$\frac{m}{2}$����m2-5m+2=0���ݴ˿ɵ�m�Ƿ���x2-5x+2=0��ʵ������
��3������ax2+bx+c=0��a��0���ɻ�Ϊx2+$\frac{b}{a}$x+$\frac{c}{a}$=0��ģ���о�С�������ɵ�һ�Թ̶�������ꣻ
��4�����跽�̵ĸ�Ϊx���������������ƿɵ�$\frac{{n}_{1}}{x-{m}_{1}}$=$\frac{{m}_{2}-x}{{n}_{2}}$�������õ�x2-��m1+m2��x+m1m2+n1n2=0���ٸ���ax2+bx+c=0���ɵ�x2+$\frac{b}{a}$x+$\frac{c}{a}$=0�����Ƚ�ϵ���ɵ�m1��n1��m2��n2��a��b��c֮��Ĺ�ϵ��
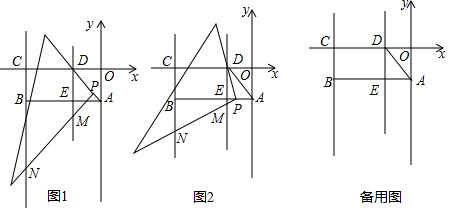
��� �⣺��1����ͼ��ʾ����D��Ϊ����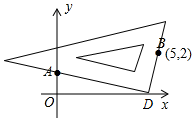
��2����ͼ��ʾ������B��BD��x���ڵ�D��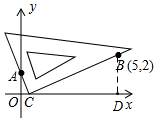
���ݡ�AOC=��CDB=90�㣬��ACO=��CBD���ɵá�AOC�ס�CDB��
��$\frac{AO}{CD}$=$\frac{OC}{BD}$��
��$\frac{1}{5-m}$=$\frac{m}{2}$��
��m��5-m��=2��
��m2-5m+2=0��
��m�Ƿ���x2-5x+2=0��ʵ������
��3������ax2+bx+c=0��a��0���ɻ�Ϊ
x2+$\frac{b}{a}$x+$\frac{c}{a}$=0��
ģ���о�С�������ɵã�A��0��1����B��-$\frac{b}{a}$��$\frac{c}{a}$����A��0��$\frac{1}{a}$����B��-$\frac{b}{a}$��c���ȣ�
��4����ͼ��P��m1��n1����Q��m2��n2����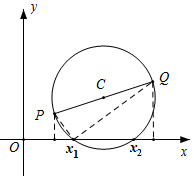
�跽�̵ĸ�Ϊx���������������ƿɵ�$\frac{{n}_{1}}{x-{m}_{1}}$=$\frac{{m}_{2}-x}{{n}_{2}}$��
��ʽ�ɻ�Ϊx2-��m1+m2��x+m1m2+n1n2=0��
�֡�ax2+bx+c=0����x2+$\frac{b}{a}$x+$\frac{c}{a}$=0��
��Ƚ�ϵ���ɵ�m1+m2=-$\frac{b}{a}$��
m1m2+n1n2=$\frac{c}{a}$��
���� ���������������ۺ��⣬��Ҫ�������һԪ���η��̵Ľ⣬���������ε��ж������ʵ��ۺ�Ӧ�ã��������Ĺؼ����������߹������������Σ��������������εĶ�Ӧ�߳ɱ������г�����ʽ��ת��Ϊ�Ȼ�ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
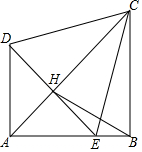 ����������Rt��ADE��Rt��ABC�����С�DAE=��ABC=90�㣬AB=BC��AD=AE����ͼ������һ�𣬵�E��AB�ϣ�AC��DE���ڵ�H������BH��CE���ҡ�BCE=15�㣬���н��ۣ�
����������Rt��ADE��Rt��ABC�����С�DAE=��ABC=90�㣬AB=BC��AD=AE����ͼ������һ�𣬵�E��AB�ϣ�AC��DE���ڵ�H������BH��CE���ҡ�BCE=15�㣬���н��ۣ�| A�� | ֻ�Т٢� | B�� | ֻ�Тۢ� | C�� | ֻ�Т٢ڢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC����������O��ʹ�á�O����A��C���㣬��Բ��O����AB���ϣ���Ҫ�߹���ͼ��������ͼ�ۼ�����д������
��ͼ����֪��ABC����������O��ʹ�á�O����A��C���㣬��Բ��O����AB���ϣ���Ҫ�߹���ͼ��������ͼ�ۼ�����д�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
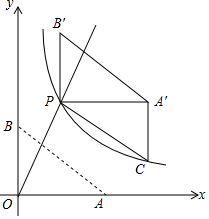 ��ͼ��ֱ��y=k1x��x��0����˫����y=$\frac{k_2}{x}$��x��0���ཻ�ڵ�P��2��4������֪��A��4��0����B��0��3��������AB����Rt��AOB��OP����ƽ�ƣ�ʹ��O�ƶ�����P���õ���A'PB'������A'��A'C��y�ύ˫�����ڵ�C��
��ͼ��ֱ��y=k1x��x��0����˫����y=$\frac{k_2}{x}$��x��0���ཻ�ڵ�P��2��4������֪��A��4��0����B��0��3��������AB����Rt��AOB��OP����ƽ�ƣ�ʹ��O�ƶ�����P���õ���A'PB'������A'��A'C��y�ύ˫�����ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
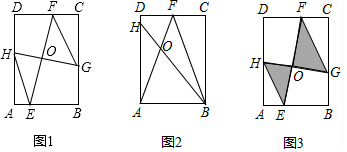
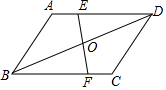 ��ͼ����?ABCD�У���E��F�ֱ���AD��BC�ϣ���AE=CF��EF��BD�ཻ�ڵ�O����֤��OE=OF��
��ͼ����?ABCD�У���E��F�ֱ���AD��BC�ϣ���AE=CF��EF��BD�ཻ�ڵ�O����֤��OE=OF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com