
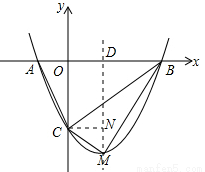
(12分)如图,抛物线y=mx2―2mx―3m(m>0)与x轴交于A、B两点, 与y轴交于C点。

(1)请求抛物线顶点M的坐标(用含m的代数式表示),A,B两点的坐标;(6分)
(2)经探究可知,△BCM与△ABC的面积比不变,试求出这个比值;(6分)
(1)M的坐标为(1, m),A,B两点的坐标为(-1,0)、(3,0) (2)1:2
m),A,B两点的坐标为(-1,0)、(3,0) (2)1:2
【解析】
试题分析:(1)将抛物线的解析式化为顶点坐标式,即可得到顶点M的坐标;抛物线的解析式中,令y=0,可求得A、B的坐标.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比
试题解析:(1)∵y=mx2―2mx―3m=m(x2―2x―3)=m(x-1)2―4m,
∴抛物线顶点M的坐标为(1,-4m),
∵抛物线y=mx2―2mx―3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2―2mx―3m=0,
∵m>0,
∴x2―2x―3=0,
解得x1=-1,x,2=3,
∴A,B两点的坐标为(-1,0)、(3,0).
(2)当x=0时,y=―3m,
∴点C的坐标为(0,-3m),
∴S△ABC=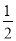 ×|3-(-1)|×|-3m|=6|m|=6m,
×|3-(-1)|×|-3m|=6|m|=6m,
过点M作MD⊥x轴于D,
则OD=1,BD=OB-OD=2,
MD=|-4m |=4m.
∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
=
=3m.
∴S△BCM:S△ABC=1:2
考点:二次函数的综合题
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省泰州市海陵区七年级上学期中质量调研数学试卷(解析版) 题型:选择题
下列各数中,是负数的是( ).
A.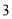 B.0 C.
B.0 C. D.2014
D.2014
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃省嘉峪关市七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列说法正确的是( )
①0是绝对值最小的有理数
②相反数大于本身的数是负数
③数轴上原点两侧的数互为相反数
④两个数比较,绝对值大的反而小.
A.①② B.①③ C.①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山西农业大学附属中学九年级上学期期末考试数学试卷(解析版) 题型:解答题
(8分)商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价x元。据此规律,请回答:
(1)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);(2分)
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?(6分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山西农业大学附属中学九年级上学期期末考试数学试卷(解析版) 题型:填空题
在比例尺为1∶10000000的地图上,量得甲、乙两地的距离是30cm,则两地的实际距离为 km。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省九年级下学期开学考试数学试卷(解析版) 题型:解答题
某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图(题22-1图)补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山西省大同市矿区七年级上学期期末质量检测数学试卷(解析版) 题型:选择题
一个多项式与 的和是
的和是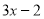 ,则这个多项式为( )
,则这个多项式为( )
(A) (B)
(B)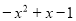
(C) (D)
(D)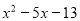
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com