

���� ���ݽ�ƽ���ߵ����ʡ��߶εĴ�ֱƽ���ߵ����ʼ��ɽ�����⣮
��� �⣺�ߵ�P�ڡ�ABC��ƽ�����ϣ�
���P����ABC���ߵľ�����ȣ���ƽ�����ϵĵ㵽�ǵ����߾�����ȣ���
�ߵ�P���߶�BD�Ĵ�ֱƽ�����ϣ�
��PB=PD���߶εĴ�ֱƽ�����ϵĵ㵽�߶ε������˵�ľ�����ȣ���
�ʴ�Ϊ��ƽ�����ϵĵ㵽�ǵ����߾�����Ȼ��߶εĴ�ֱƽ�����ϵĵ㵽�߶ε������˵�ľ�����ȣ�
���� ���⿼����ͼ-������ͼ����ƽ���ߵ����ʡ��߶εĴ�ֱƽ���ߵ����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬���ڻ����⣬�п��������ͣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
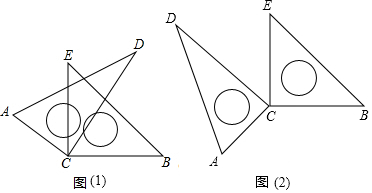
 ��������������ͼ��ʾ����Ӧ���ϣ�Ȧ���ڣ�
��������������ͼ��ʾ����Ӧ���ϣ�Ȧ���ڣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 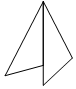 | B�� | 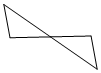 | C�� | 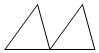 | D�� | 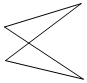 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ѧ��ȫ�������ε��ж���С����������һ����Ŀ������֪����ͼ��AB=AC��AD=AE����AEC=��ADB����֤����ABD�ա�ACE������ʦ˵������֪���������ˣ���ô����ȥ����һ����֪�����ǣ���AEC=��ADB��ȥ�������������������֤����
ѧ��ȫ�������ε��ж���С����������һ����Ŀ������֪����ͼ��AB=AC��AD=AE����AEC=��ADB����֤����ABD�ա�ACE������ʦ˵������֪���������ˣ���ô����ȥ����һ����֪�����ǣ���AEC=��ADB��ȥ�������������������֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a+c}{a+b}=\frac{c}{b}$ | B�� | $\frac{a-c}{-a+b}=-\frac{a-c}{a+b}$ | ||
| C�� | $\frac{x^8}{x^2}={x^4}$ | D�� | $\frac{b}{{3{a^2}}}+\frac{1}{6ab}=\frac{{2{b^2}+a}}{{6{a^2}b}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com