
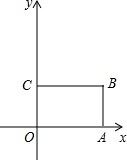
 如图所示,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,且B(2,1).矩形OABC绕点O按逆时针方向旋转90°后得到矩形ODEF.抛物线y=-
如图所示,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,且B(2,1).矩形OABC绕点O按逆时针方向旋转90°后得到矩形ODEF.抛物线y=-| 1 | 4 |
 解:(1)∵B(2,1),
解:(1)∵B(2,1),| 1 |
| 4 |
|
|
| 1 |
| 4 |
| 1 |
| 12 |
| 13 |
| 6 |
| 1 |
| 4 |
| 1 |
| 12 |
| 13 |
| 6 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
| 9 | x |
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.查看答案和解析>>
科目:初中数学 来源: 题型:
 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
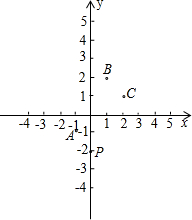 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
 BE.
BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com