
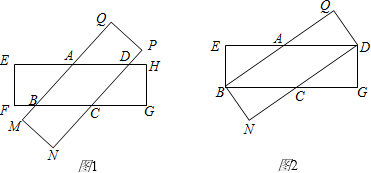
 已知有两张全等的矩形纸片.
已知有两张全等的矩形纸片.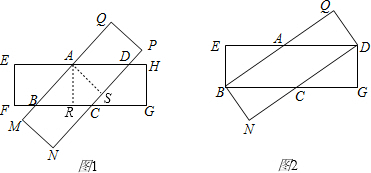 解:(1)四边形ABCD是菱形.
解:(1)四边形ABCD是菱形.| 15 |
| 4 |
| 45 |
| 4 |


科目:初中数学 来源: 题型:
已知有两张全等的矩形纸片.
(1)将两张纸片叠合成如图1,请判断四边形ABCD的形状,并说明理由;
(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图2时,菱形的面积最大,求此时菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省扬州市八年级上学期期末数学试卷(带解析) 题型:解答题
已知有两张全等的矩形纸片。
(1)将两张纸片叠合成如图甲,请判断四边形 的形状,并说明理由;
的形状,并说明理由;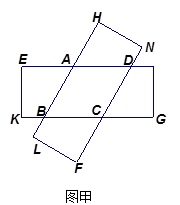
(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图乙时,菱形的面积最大,求此时菱形 的面积.
的面积.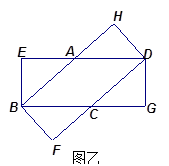
查看答案和解析>>
科目:初中数学 来源:2011届福建省晋江市初三上学期末数学卷 题型:解答题
已知有两张全等的矩形纸片.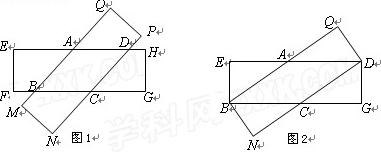
(1)将两张纸片叠合成如图1,请判断四边形ABCD的形状,并说明理由;
(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图2时,菱形的面积最大,求此时菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省扬州市八年级上学期期末数学试卷(解析版) 题型:解答题
已知有两张全等的矩形纸片。
(1)将两张纸片叠合成如图甲,请判断四边形 的形状,并说明理由;
的形状,并说明理由;
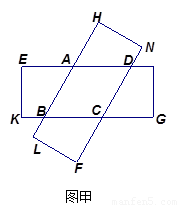
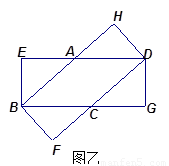
(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图乙时,菱形的面积最大,求此时菱形 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com