
 已知正方形ABCD的边长为3,E是BC上一点,BE=$\sqrt{3}$,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( )
已知正方形ABCD的边长为3,E是BC上一点,BE=$\sqrt{3}$,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( )| A. | 3$\sqrt{3}$-3 | B. | 3-$\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
分析 先求得AE和CE的长,然后由翻折的性质得到PE=EC,最后根据当点A、P、E一条直线上时,AP有最小值求解即可.
解答 解:如图所示: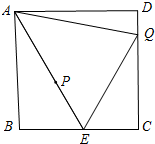
在Rt△ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$.
∵BC=3,BE=$\sqrt{3}$,
∴EC=3-$\sqrt{3}$.
由翻折的性质可知:PE=CE=3-$\sqrt{3}$.
∵AP+PE≥AE,
∴AP≥AE-PE.
∴当点A、P、E一条直线上时,AP有最小值.
∵tan∠AEB=$\frac{AB}{BE}$=$\sqrt{3}$,
∴∠BEA=60°.
∴∠CEQ=60°.
∴QC=$\sqrt{3}$EC=3$\sqrt{3}$-3.
故选:A.
点评 本题主要考查的是翻折的性质、勾股定理的应用,明确当点A、P、E在一条直线上时,AP有最小值是解题的关键.


科目:初中数学 来源: 题型:解答题
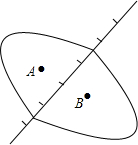 如图是王先生祖居的位置图,由于保存不慎已残缺不全,但可知钟楼的坐标为A(5,-2),街口坐标为B(5,2),资料记载王先生祖居的老屋坐标为(1,1),你能帮王先生找到祖居的老屋吗?
如图是王先生祖居的位置图,由于保存不慎已残缺不全,但可知钟楼的坐标为A(5,-2),街口坐标为B(5,2),资料记载王先生祖居的老屋坐标为(1,1),你能帮王先生找到祖居的老屋吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com