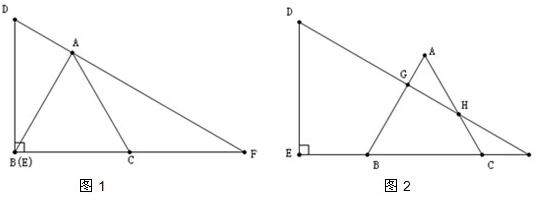
(1)①证明:∵△ABC和△ADF都是等边三角形
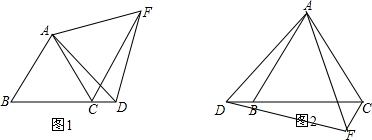
,
∴AB=AC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠CAD=∠DAF+∠CAD,
即∠BAD=∠CAF,
在△ABD和△ACF中
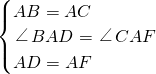
,
∴△ABD≌△ACF,
∴BF=CF;
②解:∵△ABD≌△ACF,
∴∠ACF=∠ABD=60°,
又∵∠ACB=60°,
∴∠FCD=180°-(∠ACB+∠ACF)=60°;
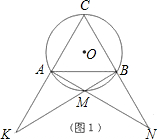
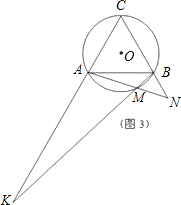
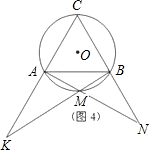
(2)解:如图;
∵△ABC和△ADF都是等边三角,
∴AB=AC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC-∠BAF=∠DAF+∠BAF,
即∠BAD=∠CAF,
在△ABD和△ACF中
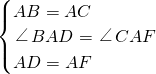
,
∴△ABD≌△ACF,
∴∠ADB=∠AFC,∠DAB=∠FCA,
∴∠AFC+∠DAC=∠ADB+∠DAB+∠BAC=∠ABC+∠BAC=60°+60°=120°.
故答案为∠AFC+∠DAC=120°.
分析:(1)①根据等边三角形的性质得AB=AC,AD=AF,∠BAC=∠DAF=60°,则∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,根据全等三角形的判定方法得到△ABD≌△ACF,
则BF=CF;②由△ABD≌△ACF得到∠ACF=∠ABD=60°,然后利用∠FCD=180°-(∠ACB+∠ACF)进行计算;
(2)根据题意画图,与①一样可证明△ABD≌△ACF,则∠ADB=∠AFC,∠DAB=∠FCA,于是∠AFC+∠DAC=∠ADB+∠DAB+∠BAC=∠ABC+∠BAC=60°+60°=120°.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等,对应角相等.也考查了等边三角形的性质.

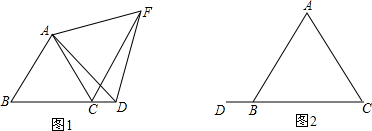
 ,
, ,
, ,
,





 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
