
 如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.分析 (1)连接CE,由AE是⊙O的直径,得到CE⊥AD,根据等腰三角形的性质得到∠AEC=∠DEC,于是得到结论;
(2)连接BC,OB,OC,由已知条件得到△AED是等边三角形,得到∠A=60°,推出AE∥BC,∠BOC=60°,于是得到结论.
解答 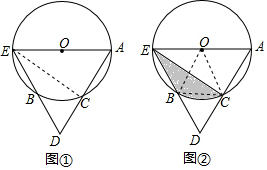 解:(1)连接CE,
解:(1)连接CE,
∵AE是⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴AE=ED,
∴∠AEC=∠DEC,
∴$\widehat{BC}=\widehat{AC}$;
∴点C是劣弧$\widehat{AB}$的中点;
(2)连接BC,OB,OC,
∵AE=2AC=4,
∴∠AEC=30°,AE=AD,
∴∠AED=60°,
∴△AED是等边三角形,
∴∠A=60°,
∵$\widehat{BC}$=$\widehat{AC}$,
∴$\widehat{BE}$=$\widehat{BC}$=$\widehat{AC}$,
∴AE∥BC,∠BOC=60°,
∴S△OBC=S△EBC,
∴S阴影=S扇形=$\frac{60•π×{2}^{2}}{360}$=$\frac{2}{3}$π.
点评 本题考查了等边三角形的判定和性质,圆周角定理,平行线的判定,扇形的面积的计算,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
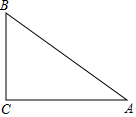 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D,E分别在边AB,AC上,将△ADE沿直线DE翻折,点A的对应点在边AB上,联结A′C,如果A′C=A′A,那么BD=$\frac{15}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D,E分别在边AB,AC上,将△ADE沿直线DE翻折,点A的对应点在边AB上,联结A′C,如果A′C=A′A,那么BD=$\frac{15}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
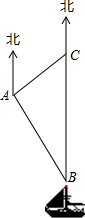 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至海面B处时,测得该岛位于正北方向25海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西33°的方向上,求A,C之间的距离.(参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649,$\sqrt{2}$≈1.414,结果保留一位小数)
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至海面B处时,测得该岛位于正北方向25海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西33°的方向上,求A,C之间的距离.(参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649,$\sqrt{2}$≈1.414,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
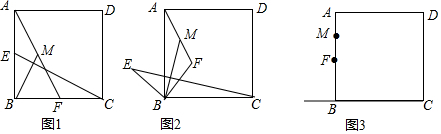
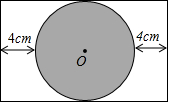 电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.
电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com