
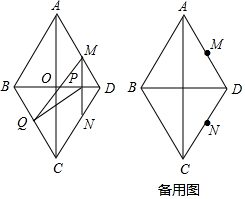
 已知:如图,菱形ABCD中,AB=10cm,BD=12cm,对角线AC与BD相交于点O,直线MN以1cm/s从点D出发,沿DB方向匀速运动,运动过程中始终保持MN⊥BD,垂足是点P,过点P作PQ⊥BC,交BC于点Q.(0<t<6)
已知:如图,菱形ABCD中,AB=10cm,BD=12cm,对角线AC与BD相交于点O,直线MN以1cm/s从点D出发,沿DB方向匀速运动,运动过程中始终保持MN⊥BD,垂足是点P,过点P作PQ⊥BC,交BC于点Q.(0<t<6)分析 (1)如图1中,在Rt△BOC中,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,推出sin∠OBC=$\frac{OC}{BC}$=$\frac{4}{5}$,在Rt△PBQ中,由PB=12-t推出sin∠PBQ=$\frac{PQ}{PB}$=$\frac{4}{5}$,即可求出PQ.
(2)如图2中,作QH⊥MN于H.求出QH、PM即可解决问题.
(3)如图3中,连接QN只要证明QM经过点O时,OP是△MQN的中位线,得到QN=2OP,由此列出方程即可解决问题.
解答 解:(1)如图1中,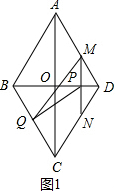
∵四边形ABCD是菱形,
∴BC=AB=10,OB=OD=6,BD⊥AC,
在Rt△BOC中,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴sin∠OBC=$\frac{OC}{BC}$=$\frac{4}{5}$,
在Rt△PBQ中,∵PB=12-t,
sin∠PBQ=$\frac{PQ}{PB}$=$\frac{4}{5}$,
∴PQ=$\frac{4}{5}$(12-t)=$\frac{48}{5}$-$\frac{4}{5}$t(0<t<6).
(2)如图2中,作QH⊥MN于H.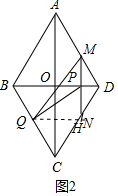
∵∠QPH+∠BPQ=90°,∠BPQ+∠CBO=90°,
∴∠QPH=∠CBO,
∴QH=PQ•sin∠QPH=$\frac{4}{5}$($\frac{48}{5}$-$\frac{4}{5}$t),
易知PM=$\frac{4}{3}$t,
∴y=$\frac{1}{2}$•PM•QH=$\frac{1}{2}$•$\frac{4}{3}$t•$\frac{4}{5}$($\frac{48}{5}$-$\frac{4}{5}$t)=$\frac{384}{75}$-$\frac{32}{75}$t(0<t<6).
(3)如图3中,连接QN.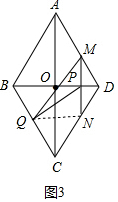
当MQ经过点O时,易证△BOQ≌△DOM,
∴BQ=DM,OM=OQ,
∵PM=PN,
∴OP∥QN,NQ=2OP,
∴QN⊥MN,QN=$\frac{4}{5}$($\frac{48}{5}$-$\frac{4}{5}$t),
∴$\frac{4}{5}$($\frac{48}{5}$-$\frac{4}{5}$t)=2(6-t),
解得t=$\frac{54}{17}$,
∴t=$\frac{54}{17}$时,MQ经过点O.
点评 本题考查四边形综合题、菱形的性质、时间中位线定理、锐角三角函数、勾股定理、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,熟练应用锐角三角函数解决问题,属于中考压轴题.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
| 品名 | 西红柿 | 豆角 |
| 批发价(单位:元/kg) | 2.4 | 3.2 |
| 零售价(单位:元/kg) | 3.8 | 5.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2500(1+x)2=3600 | B. | 2500+2500(1+x)+2500(1+x)2=3600 | ||
| C. | 2500(1-x)2=3600 | D. | 2500(1+x)+2500(1+x)2=3600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
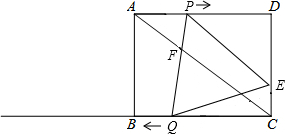 如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s;同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,过点P作PE∥AC交DC于点E,连接PQ、QE,PQ交AC于F.设运动时间为t(s)(0<t<8),解答下列问题:
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s;同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,过点P作PE∥AC交DC于点E,连接PQ、QE,PQ交AC于F.设运动时间为t(s)(0<t<8),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9的立方根是3 | |
| B. | 每一个实数都可以用数轴上的点来表示 | |
| C. | 带根号的数是无理数 | |
| D. | 两条直线被第三条直线所截,同旁内角互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
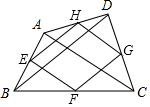 如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )
如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )| A. | AB∥DC | B. | AD=BC | C. | AC⊥BD | D. | AC=BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com