
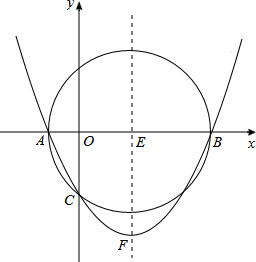 如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.
如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.分析 (1)由题意可直接得到点A、B的坐标,连接CE,在Rt△OCE中,利用勾股定理求出OC的长,则得到点C的坐标;
(2)已知点A、B、C的坐标,利用交点式与待定系数法求出抛物线的解析式,由解析式得到顶点F的坐标;
(3)首先求出点P的坐标;连接EP,PF,过点P作PG⊥对称轴EF于点G,求出PE,推出点P在⊙E上;再利用勾股定理求出PF的长度,则利用勾股定理的逆定理可判定△EPF为直角三角形,∠EPF=90°,所以直线PF与⊙E相切.
解答 解:(1)∵以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,
∴A(-2,0),B(8,0).
如解答图所示,连接CE.
在Rt△OCE中,OE=AE-OA=5-2=3,CE=5,
由勾股定理得:OC=$\sqrt{C{E}^{2}-O{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴C(0,-4).
(2)∵点A(-2,0),B(8,0)在抛物线上,
∴可设抛物线的解析式为:y=a(x+2)(x-8).
∵点C(0,-4)在抛物线上,
∴-4=a×2×-8,解得a=$\frac{1}{4}$
∴抛物线的解析式为:y=$\frac{1}{4}$(x+2)(x-8)=$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{1}{4}$(x-3)2-$\frac{25}{4}$,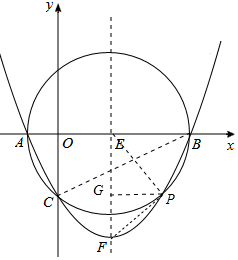
∴顶点F的坐标为(3,-$\frac{25}{4}$).
(3)直线PF与⊙E相切.理由如下:
∵△ABC中,底边AB上的高OC=4,
∴若△ABC与△ABP面积相等,则抛物线上的点P须满足条件:|yP|=4,
∵点P在第四象限,
∴yp=-4,则 $\frac{1}{4}$x2-$\frac{3}{2}$x-4=-4,
整理得:x2-6x=0,解得x=6或x=0(与点C重合,故舍去).
∴点P的坐标为(6,-4),连接EP,PF,过点P作PG⊥对称轴EF于点G,
则PG=3,EG=4.
在Rt△PEG中,由勾股定理得:PE=$\sqrt{E{G}^{2}+P{G}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴点P在⊙E上.
由(2)知,顶点F的坐标(3,-$\frac{25}{4}$),
∴EF=$\frac{25}{4}$,
∴FG=EF-EG=$\frac{9}{4}$.
在Rt△PGF中,由勾股定理得:PF=$\sqrt{P{G}^{2}+G{F}^{2}}$=$\sqrt{{3}^{2}+(\frac{9}{4})^{2}}$=$\frac{15}{4}$.
在△EFP中,∵EP2+PF2=52+( $\frac{15}{4}$)2=( $\frac{25}{4}$)2=EF2,
∴△EFP为直角三角形,∠EPF=90°.
∵点P在⊙E上,且∠EPF=90°,
∴直线PF与⊙E相切.
点评 本题考查圆综合题、二次函数的图象与性质、勾股定理及其逆定理、切线的判定、解一元二次方程等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形,掌握利用勾股定理的逆定理证明直角的方法,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
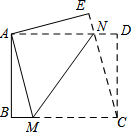 如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )
如图,在长方形ABCD中,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN,若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为( )| A. | 5 | B. | 4 | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com