
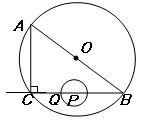
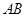 与⊙P相切.
与⊙P相切.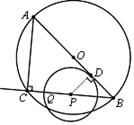
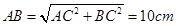 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.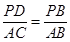 ,即
,即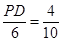 ,∴PD ="2.4(cm)" .
,∴PD ="2.4(cm)" .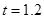 时,
时,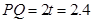 (cm)
(cm) 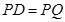 ,即圆心
,即圆心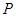 到直线
到直线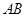 的距离等于⊙P的半径.
的距离等于⊙P的半径. 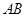 与⊙P相切.
与⊙P相切.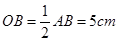 .
.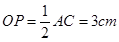 .
. 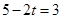 或
或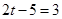 ,∴
,∴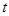 =1或4.
=1或4. 

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源:不详 题型:解答题
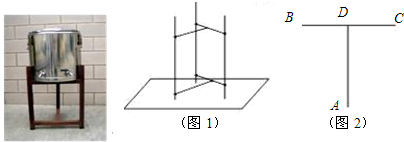
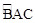 的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。
的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。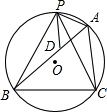
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
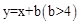 与x轴、y轴分别相交于点A、B,与正比例函数
与x轴、y轴分别相交于点A、B,与正比例函数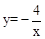 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。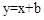 与⊙O有哪些位置关系?求出相应b的取值范围。
与⊙O有哪些位置关系?求出相应b的取值范围。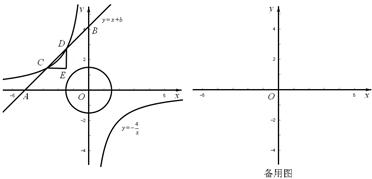
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
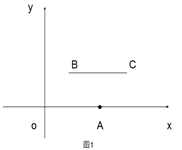
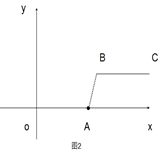

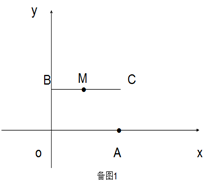
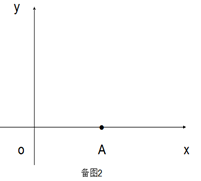
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com