C
分析:正多边形,每边都相等,因为有20个等分点,所以边数是20的约数.分解20=2×2×5,约数有1,2,4,5,10,20共6个,排除1和2,符合条件的正多边形共有四种:正四边形、正五边形、正十边形和正二十边形.
解答:设正k边形满足条件,则除去k个顶点外的20-k个点均匀地分布在正k边形各边所对的劣弧上,
于是
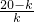
=
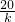
-1是整数,
故
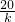
是整数,
但k≥3,
∴k=4或5或10或20.
∴正多边形的个数有
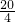
+
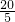
+

+
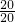
=12.
故选C.
点评:本题考查了正多边形的判定和性质,解题关键是由除去k个顶点外的20-k个点均匀地分布在正k边形各边所对的劣弧上,得出边数是20的约数.

 阅读快车系列答案
阅读快车系列答案