
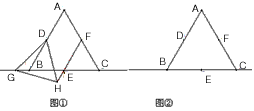
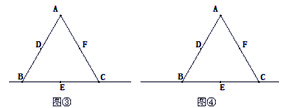
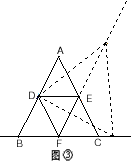
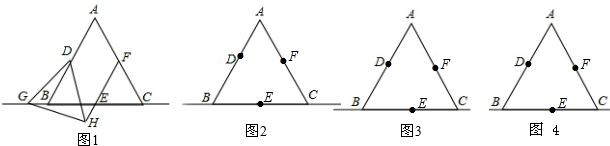
| 证明:连接DE、EF、DF; (1)当点G在线段BE上时,如图①, 在EF上截取EH使EH=BG, ∵D、E、F是等边△ABC三边中点, ∴△DEF、△DBE也是等边三角形且DE=AB=  BD BD在△DBG和△DEH中, 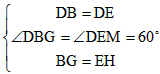 , ,∴△DBG≌△DEH, ∴DG=DH, ∴∠BDG=∠EDH, ∵∠BDE=∠GDE+∠BDG=60°, ∴∠GDH=∠GDE+∠EDH=60°, ∴在直线EF上存在点H使得△DGH是等边三角形; (2)当点G在射线EC上时,如图②,在EF上截取EH使EH=BG, 由(1)可证△DBG≌△DEH, ∴DG=DH,∠BDG=∠EDH, ∵∠BDE=∠BDG-∠EDG=60°, ∴∠GDH=∠EDH-∠EDG=60°, ∴在直线EF上存在点H使得△DGH是等边三角形; (3)当点G在BC延长线上时,如图③, 与(2)同理可证,结论成立; 综上所述,点G在直线BC上的任意位置时,该结论成立。 |
   |


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:在等边△ABC中,AB、cosB是关于x的方程x2-4mx-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江东阳歌山一中八年级第一次月考数学试卷(带解析) 题型:解答题
如图,已知:在等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD相交于点P.
(1)说明△ADC≌△CEB的理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江东阳歌山一中八年级第一次月考数学试卷(解析版) 题型:解答题
如图,已知:在等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD相交于点P.
(1)说明△ADC≌△CEB的理由;
(2)求∠BPC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
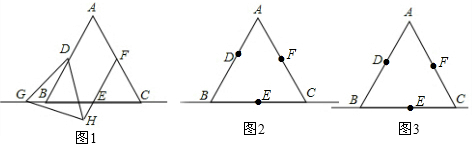
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com